【2017年前期・千葉県公立高校入試数学】第2問(5)（作図）問題・解答・解説

【はじめに】私は、様々な理由で受験や進学で不利になっている子どもたち（原発被災避難世帯、児童養護施設、母子生活支援施設、ひとり親家庭など）の学習サポートを続けてまいりました。しかし直接伺える場所・教えられる子どもの数は限られますので、どなたでもご覧いただけるように、公式サイトにその内容をUPすることにいたしました。どうぞご活用ください。入試問題は実際は、白黒です。ただせっかくの画像上ですので、一部カラーにしました。

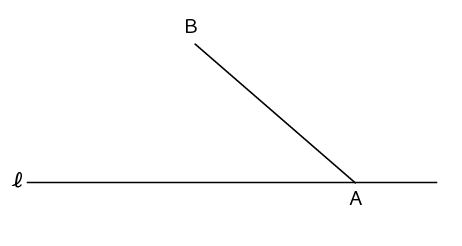
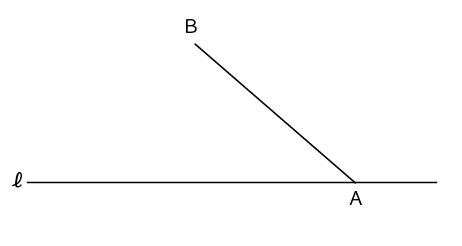
【2017年前期・数学・第２問（5）（作図）問題】（5点）
下の図のように、線分ABと、点Ａを通る直線ℓがある。円Ｏは、線分AB上に中心があり、直線ℓに接し、さらに、円周上に点Ｂがある。このとき、円Ｏを作図によって求めなさい。また、円Ｏの中心の位置を示す文字Ｏも書きなさい。ただし、三角定規の角を利用して直線をひくことはしないものとし、作図に用いた線は消さずに残しておくこと。

[next_p]