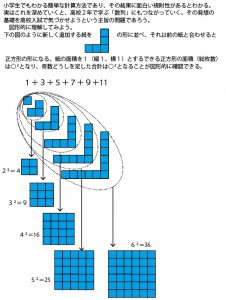
2018年2月13日、千葉県公立高校前期入試「数学」第3問（二次関数）問題・解答・解説（速報）

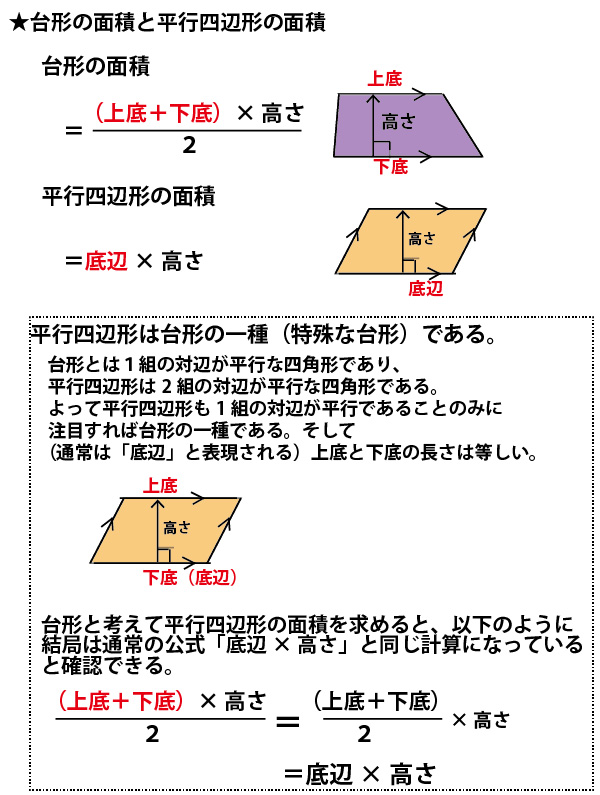
後日追記。その後、解説動画も作成しました。以下の静止画での解答解説と合わせてご覧ください。

https://www.youtube.com/watch?v=BEg5ODLDZsc

2月14日午後８時30分　船橋市議・予備校講師　朝倉幹晴

船橋市も含む千葉県の中３生の皆さん。昨日（2月13日）の千葉県公立高校前期入試（学力考査）と本日（14日）の面接お疲れ様でした。今日の午後からは友達に会ったりして少し気分転換できたでしょうか？　前期での合格を祈りながらも、念のため後期に向けた勉強を始めましょう。作成に時間がかかり、翌日となってしまいましたが、数学第３問（二次関数）の解答解説速報を作成しました。

前期でできなかった部分を振り返ることでもし後期まで受験することになった場合は得点増できるようにしましょう。すでに本日の朝刊の折り込みで正解は出ています。前期にはできなかった問題も解答にいたる流れを理解すれば、後期では同様な問題を解くことができるようになります。特に苦手とする方が多い、二次関数とそれに関連する図形の読み方を説明しました。ぜひご活用しください。

（また中１、２の皆さんは、来年以降、自らが受ける入試に向けて、問題に挑戦してみませんか。中３で学ぶニ次関数は未習ですが、後半は小学校で学んだ図形の面積の活用も出てきます。未習で理解できない部分は読み飛ばしていいので、理解できる部分だけでも読んでみてください。。また大人の方も、こんな中学生たちが取り込んでいる問題にぜひ挑戦してみてください。）

 

なお、試験問題は白黒ですが、画面上ですので一部カラーにし、また各小問の配点も明記しました。

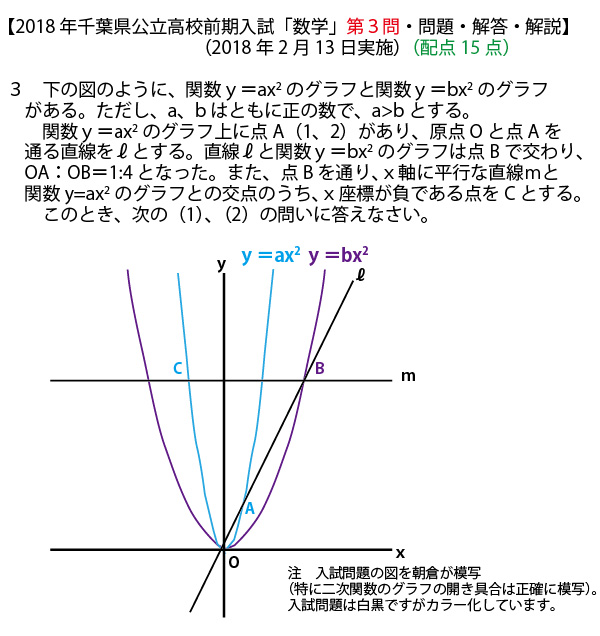
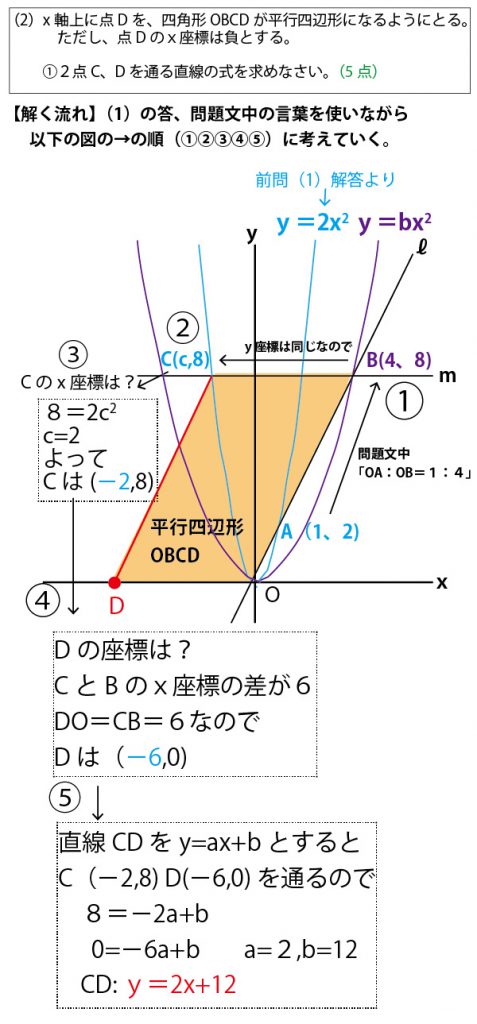
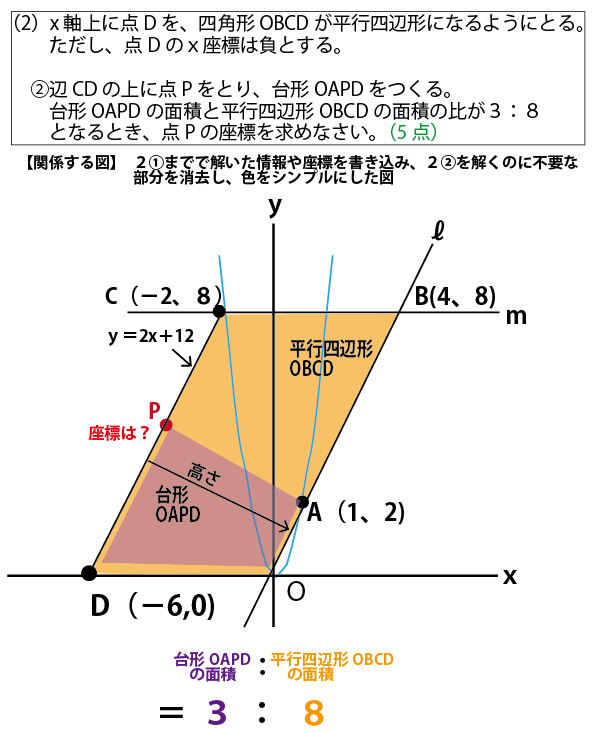
上の図を見ながら確認してほしい。

流れ①　OA：OB＝１：４だから、Bの座標はA（1，2）のｘ座標、ｙ座標それぞれ4倍なのでB（４，８）

流れ②　ｘ軸に平行な直線ｍ上の点はｙ座標は全てBと同じ８である。それがｙ＝2×2（２かけるｘの２乗）と交わる点がCであり、Cのｙ座標は８である。

流れ③　ｙ＝２x2（２かけるｘの２乗）のｙに８を代入し、Cのｘ座標が、ｘ座標が−の領域なので−２となり、Cの座標が（−２、８）とわかる。

流れ④　平行四辺形OBCDで対辺の長さは等しいので、CB＝DO。CBの長さはCとBのｘ座標−２と４の差なので６となり、CB＝DO＝６。

よってDの座標は（－６、０）となる。

流れ⑤　求めるべき直線CDは、C（−２、８）、D（−６、０）を通る。CDの方程式をｙ＝ax+bとおき、２点C（−２、８）、

D（−６、０）のｘ座標、ｙ座標の値を代入し、a、bに関する連立方程式を立てる。

８＝−２a＋ｂ・・・①

０＝−6a＋ｂ・・・②

①－②より　８＝−２a−（−6a)

8=4a       a=２

これを②に代入すると　０＝−６×２＋ｂ

ｂ＝12

よって求める方程式は、ｙ＝２ｘ＋12

 

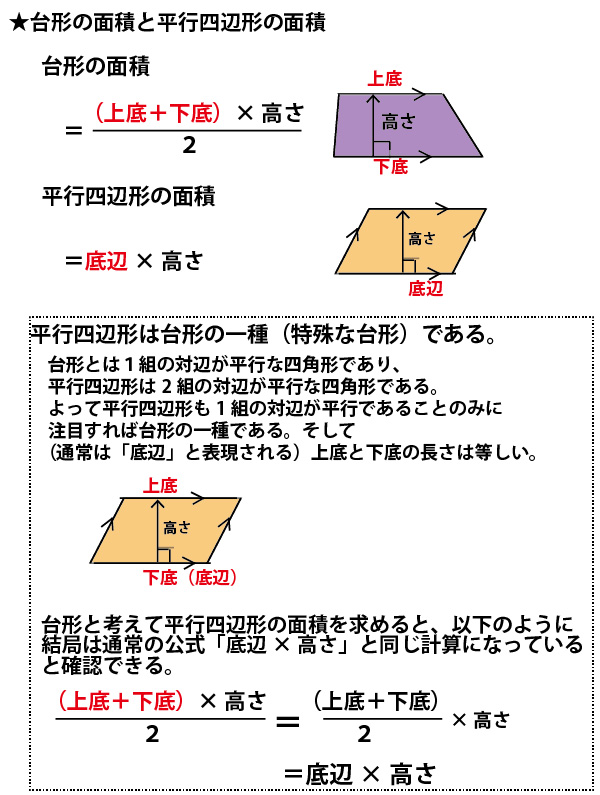
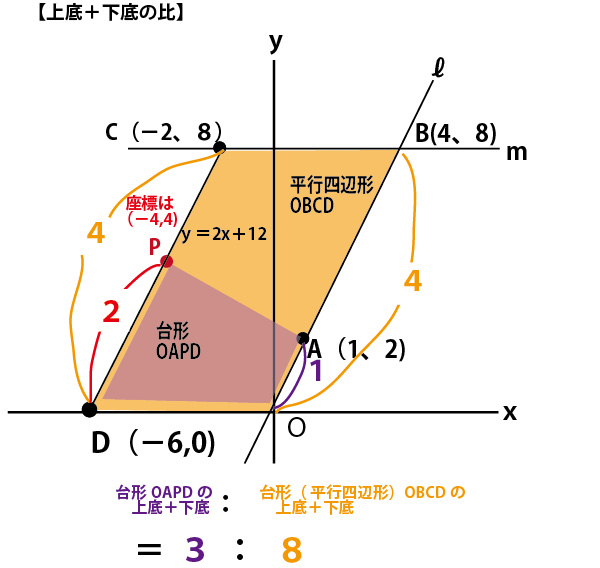
図のように台形OAPDと平行四辺形OBCDを高さが共通の台形だとみなし、DCやDPを下底、OAやODを上底とみなす。

すると「上底＋下底」の比がそのまま面積比になるので、これが、３：８になればよい。

 

問題文の本文にOA：OB＝１：４との記述があったことをそのまま活用し、OAを１と見なして考えると

台形（平行四辺形）OBCDの上底＋下底＝DC＋OB＝４＋４＝８

なので

台形OAPDの上底＋下底＝OA＋DP＝１＋DP＝３

となればよい。

すると、DP＝２、つまり、DPはDCの１／２の長さで、Pが線分CDの中点となればよい。

Pのｙ座標はCのｙ座標８とDのｙ座標０の中間なので、４となる。

ｙ＝２ｘ＋12のｙに４を代入すると、４＝２ｘ＋12　　−２ｘ＝８　ｘ＝−４

Pの座標は（−４、４）

（別解　　PはC（−２、８）、D（−６、０）の中点なので

ｘ座標　{（－２）＋（−6）}／２　＝−４

ｙ座標　（８＋０）／２　＝４

P（−４、４））