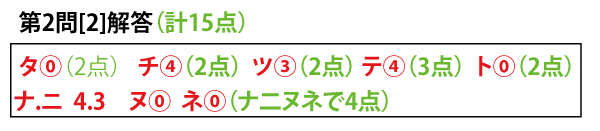
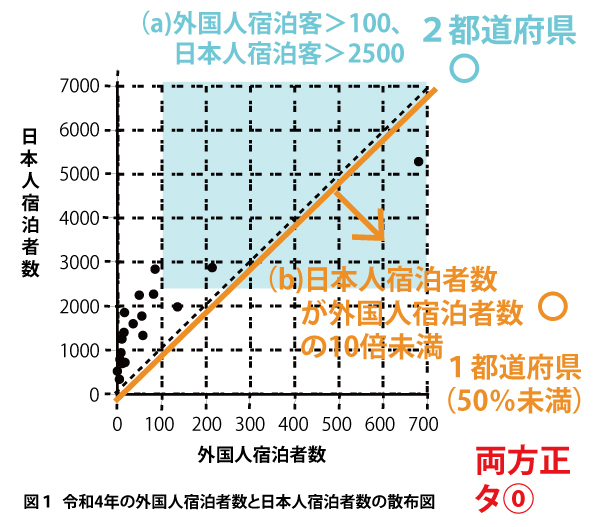
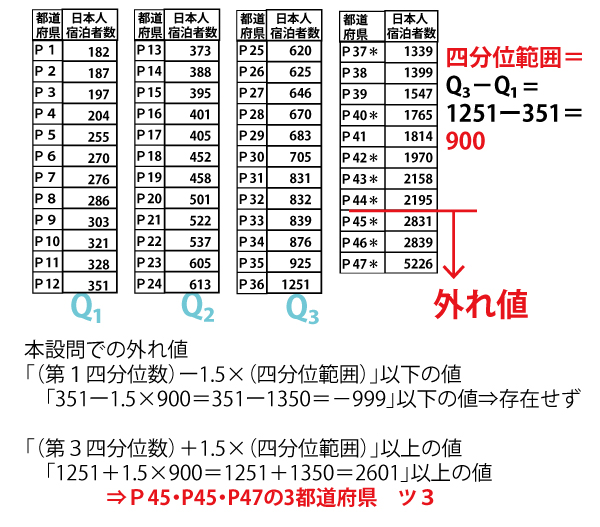
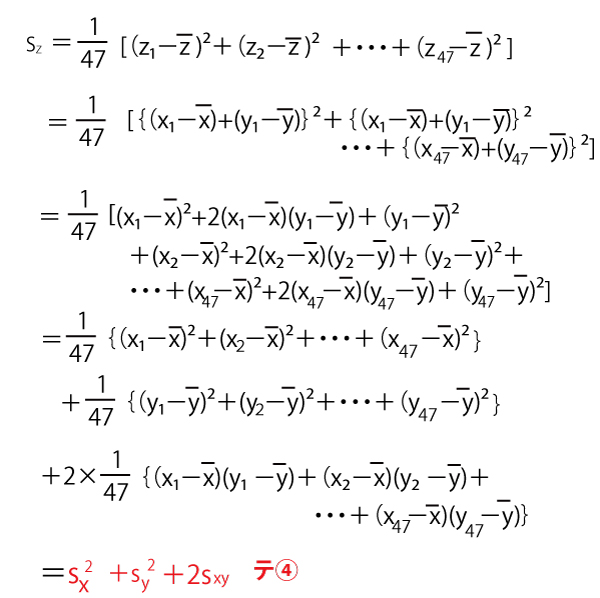2025年大学入試共通テスト「数学1A」第2問［2］（配点15点）問題・解答・解説

【解説】

（3)

太郎さんが住む地域では、その地域に宿泊を促すためのキャンペーンとして、キャンペーンA、Bが実施されている。
太郎さんは、キャンペーンAの方がよいと思っている人が多いといううわさを聞いた。このうわさのとおり、キャンペーンAの方がよいと思っている人が多いといえるかどうかを確かめることにした。そこで、かたよりなく選んだ人たちに、キャンペーンA、Bのどちらがよいかについて、二択のアンケートを行ったところ、アンケートに回答した35人のうち、23人が「キャンペーンAの方がよい」と答えた。この結果から、一般にキャンペーンAの方がよいと思っている人が多いといえるかどうかを、次の方針で考えることにした。

方針

・“「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と解答する割合は等しい”という仮説を立てる。
・この仮説のもとで、かたよりなく選ばれた35人のうち23人以上が「キャンペーンAの方がよい」と回答する確率が5％未満であれば、その仮説は誤っていると判断し、5％以上であればその仮説は誤っているとは判断しない。

後の実験結果は、35枚の硬貨を投げる実験を1000回行ったとき、表が出た枚数ごとの回数の割合を示したものである。

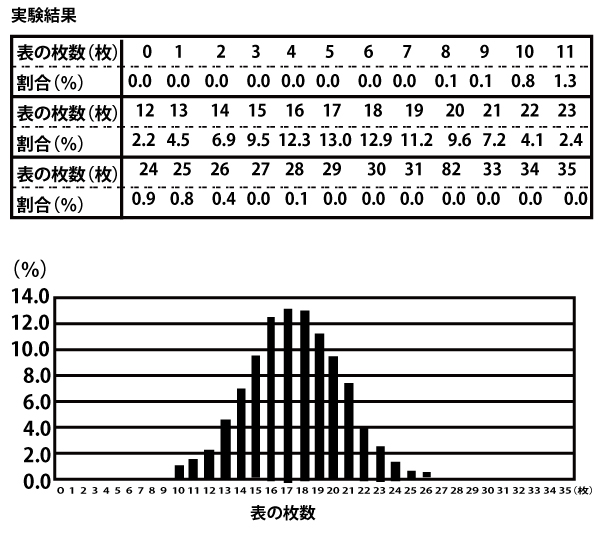23枚以上が表となった割合(%)の総計の計算式（＋0.0は省略）
2.4＋0.9＋0.5＋0.4+0.1＝4.3%（ナ.二答）
5％未満なので、“「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と解答する割合は等しい”という仮説は、誤っていると判断する（ヌ答）。したがって、今回のアンケート結果からは、キャンペーンAの方がよいと思っている人が、多いといえる（ネ答）。