2024年　＃大学入試　＃共通テスト　「＃数学IA」第5問（選択・計20点）問題・解答・解説

2024年11月26日　朝倉幹晴（予備校講師・船橋市議）

2024年大学入試共通テスト「数学１A」第5問（配点20点）の解答・解説を作成しましたので、ご活用ください。問題文の最後の所でページ番号「２」をクリックすると解答・解説に飛びます。

2024年共通テスト「数学ＩＡ」第5問（選択・計20点）

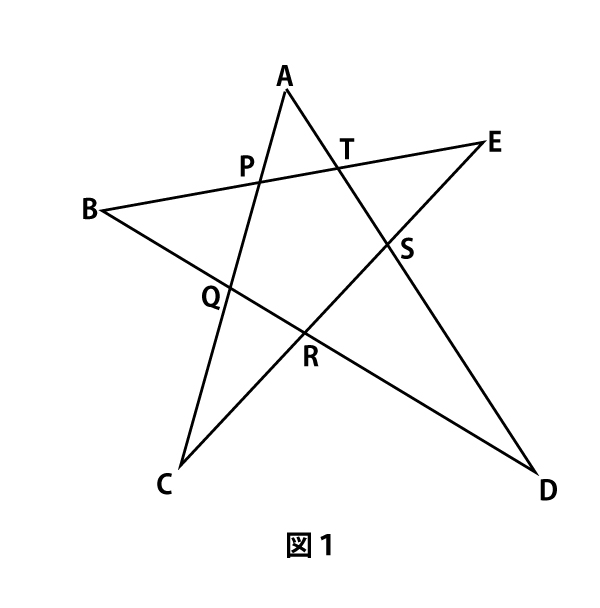
図１のように、平面上に5点A、B、C、D、Eがあり、線分AC、CE、EB、BD、DAによって、星形の図形ができるときを考える。線分ACとBEの交点をP、ACとBDの交点をQ、BDとCEの交点をQ、BDとCEの交点をR、ADとCEの交点をS、ADとBEの交点をTとする。

ここでは
AP：PQ：QC=２：３：３、

AT：TS：SD＝１：１：３
を満たす星形の図形を考える。
以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。

（1)△AQDと直線CEに着目すると

（ア2点）

が成り立つので

QR：RD＝イ：ウ（あわせて3点）

となる。また、△AQDと直線BEに着目すると

QB：BD＝エ：オ（あわせて2点）

となる。したがって

BQ：QR：RD＝エ：イ：ウ

となることがわかる。

（2）5点P、Q、R、S、Tが同一円周上にあるとし、AC＝８であるとする。
（i)5点A、P、Q、S、Tに着目すると、AT：AS＝１：２より
（3点）となる。さらに、5点D、Q、R、S、Ｔに着目すると
となる。さらに、5点D、Q、R、S、Tに着目すると
となることがわかる。

（ii）3点A、B、Cを通る円と点Dとの位置関係を、次の構想に基づいて調べよう。

構想
線分ACとBDの交点Qに着目し、AQ・CQとBQ・DQの大小を比べる。

まず、ＡＱ・ＣＱ＝5；３＝15かつＢＱ・ＤＱ＝キクであるから
ＡＱ・ＣＱケＢＱ・ＤＱ・・・・（キクケあわせて3点）

が也たる。また、3点Ａ、Ｂ、Ｃを通る円と直線ＶＤとの交点のうち、Ｂと異なる点をＸとすると
ＡＱ・ＣＱコＢＱ・ＸＱ・・・・
が也たる。の左辺は同じなので、の右辺を比べることにより、ＸＱサＤＱが得られる。したがって、点Ｄは3点A、B、Cを通る円のシにある。（コサシあわせて4点）

（iii）3点C、D、Eを通る円と2点A、Bとの位置関係について調べよう。
この星形の図形において、さらにCR=RS=SE＝3となることがわかる。したがって、点ASは3点C、D、Eを通る円のスにあり、点Bは3点C、D、Eを通る円のセにある。
（スセあわせて3点）