2021年大学入試共通テスト（第２日程）数学ⅡB問題第1問［１］「三角関数」（配点17点）問題、解答、解説

2022年6月11日　予備校講師・船橋市議（無党派）　朝倉幹晴

大学入試共通テスト数学ⅡB（第２日程）第1問[２]の問題、解答、解説を作りました。ご活用ください。

大学入試共通テスト数学ⅡB（第２日程）第1問[２]（配点17点）

座標平面上の原点を中心とする半径１の円周上に3点
P（cosθ,sinθ）,Q(cosα,sinα）,R(cosβ,sinβ）がある。ただし、０≦θ＜α＜β＜2πとする。このときｓとｔを次のように定める。
ｓ＝cosθ＋cosα＋cosβ, t=sinθ＋sinα＋sinβ

（1）△PQRが正三角形や二等辺三角形のときのsとtの値について考察しよう。

考察１　△ＰＱＲが正三角形である場合を考える。

この場合、α,βをθで表すと

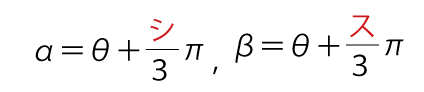
（シ1点、ス1点）
であり、加法定理により
cosα＝セ（2点）,sinα＝ソ（2点）
である。同様に、cosβおよびsinβを,sinθとcosθを用いて表すことができる。
これらのことから、s=t=タ（1点）である。

考察2　△PQRがPQ＝PRとなる二等辺三角形である場合を考える。

例えば、点Ｐが直線ｙ＝ｘ上にあり、点Ｑ,Rが直線ｙ＝ｘに関して対称であるときを考える。このとき、である。また、αは
を満たし、点Ｑ,Rの座標について、sinβ＝cosα,cosβ＝sinαが成り立つ。よって

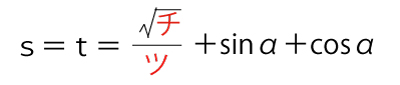
である。
ここで、三角関数の合成により

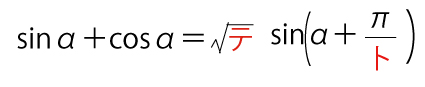
である。したがって

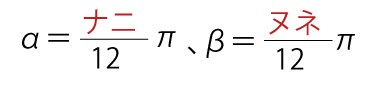
(ナニ2点）（ヌネ2点）
のとき、ｓ＝ｔ＝０である。

（2）次に、ｓとｔの値を定めたときのθ,α,βの関係について考察しよう。

考察３　ｓ＝ｔ＝０の場合を考える。

この場合、sin²θ＋cos²θ＝１により、αとβについて考えると

（ノハ－１、ヒ２、ノハヒあわせて2点）
である。
同様に、θとαについて考えると

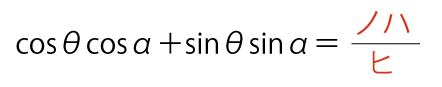
であるから、θ、α、βの範囲に注意すると

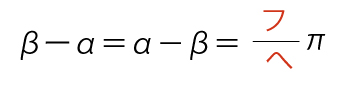
（フヘあわせて1点）
という関係が得られる。

（3）これまでの考察を振り返ると、次ののうち正しいホであることがわかる。（2点）
ホの解答群

△ＰＱＲが正三角形ならばｓ＝ｔ＝０であり、ｓ＝ｔ＝０であり、△ＰＱＲは正三角形である。
△ＰＱＲが正三角形ならばｓ＝ｔ＝０であるが、ｓ＝ｔ＝０であっても△ＰＱＲが正三角形でない場合がある。
△ＰＱＲが正三角形であってもｓ＝ｔ＝０でない場合があっても
ｓ＝ｔ＝０ならば△ＰＱＲは正三角形である。
△ＰＱＲが正三角形であってもｓ＝ｔ＝０でない場合があり
ｓ＝ｔ＝０であっても△ＰＱＲが正三角形でない場合がある。

[next_p]