2023年千葉県公立高校入試「数学」第4問（総合問題）（配点18点）問題・解答・解説

【解説】
（１）（a)

Aさんは1回目は「グーで負け」、2回目は「チョキで勝ち」、3回目は「グーで勝った」ので
－１＋２＋１＝２点

（b)６通り

      「グー勝ち」「グー勝ち」　１＋１＝1点
　　「グー勝ち」「チョキ勝ち」１＋２＝3点
　　「グー勝ち」「パー勝ち」　１＋5＝6点
　　「チョキ勝ち」「チョキ勝ち」２＋２＝4点
　　「チョキ勝ち」「パー勝ち」２＋５＝7点
　　「パー勝ち」「パー勝ち」５＋５＝10点

（c）

9点となりうるのはAさんが「パー勝ち」「パー勝ち」「グー負け」＝５＋５－１＝９の場合のみ。
すると相手のBさんは「グー負け」「グー負け」「パー勝ち」なので（－1）＋（－1）＋５＝3点

 （2）あいこは1回と数えないため、10回はAさんかBさんどちらかが必ず勝つ。（どちらかが必ず負ける）
a+b+c=10      c=10−a－b

(3) 表でAが勝った時で考え、合計点を見ると

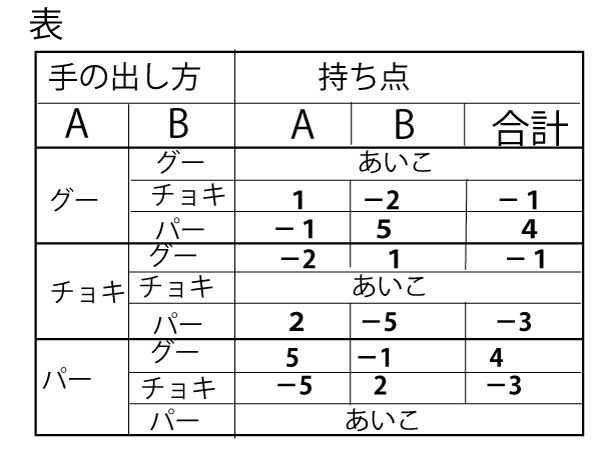
Aがグーで勝つ時は、Bはチョキで負け、合計は－１
Aがチョキで勝つ時は、Bはパーで負け、合計は－３
Aがパーで勝つ時は、Bはグーで負け、合計は４

BがAに勝った時も出し方は同じであり、合計点も同じなので、以下のように考えることができる。
どちらかがグーで勝つ時は、相手はチョキで負け、合計は－１
どちらかチョキで勝つ時は、相手はパーで負け、合計は－３
どちらかがパーで勝つ時は、相手はグーで負け、合計は４

よって2人の持ち点の合計点Ｍは
Ｍ＝a×（－1）＋ｂ×（－3）＋ｃ×４
ｃ＝10−aーbを代入して、ｃを消去すると

Ｍ＝－aー3b+4（10−a－b)
＝－aー3b+40−4a－4b
   Ｍ＝－5a－7ｂ＋40

（2）別解（総当たり的な調べ方での解答）

０＝40−5a－7b
5a＋7b＝40

a、bともに0～10の整数である。bが6以上と考えると
7bは42以上となり、式はなりたたないので
bは0,1,2,3,4,5のいずれかである。
その時、aの値が整数となるかを確かめればよい。
b=0のとき　5a＝40　a＝8　b=1のとき　5a+7=40　5a＝33 で
aは整数値とならないのであてはらない。
b=2のとき　5a＋14＝40　5a＝26で
aは整数値とならないのであてはらない。　 b=3のとき　5a+21＝40 5a＝19で
aは整数値とならないのであてはらない。
b=4のとき　5a＋28＝40　5a=12でaは整数値とならないのであてはらない。
b=5のとき　5a＋35＝40　5a=5で　a=1
c=10−a−bなので
（a,b,c)=(8,0,2)（1,5,4）の2通り