2023年千葉県公立高校入試「数学」第3問（図形の証明）（配点16点）問題・解答・解説

2023年8月26日　船橋市議・予備校講師　朝倉幹晴

2023年2月に実施された千葉県公立高校入試「数学」第3問（図形の証明）（16点）の解答・解説を作成しました。また千葉県教育委員会が発表した正答率・無答率も付記しました。学習や入試対策にご活用ください。

2023年第3問（16点）

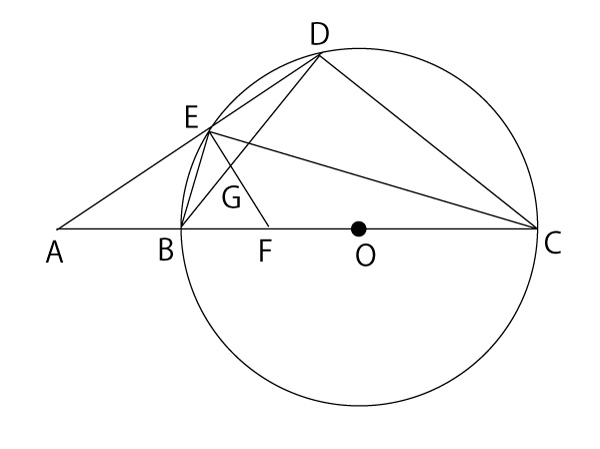
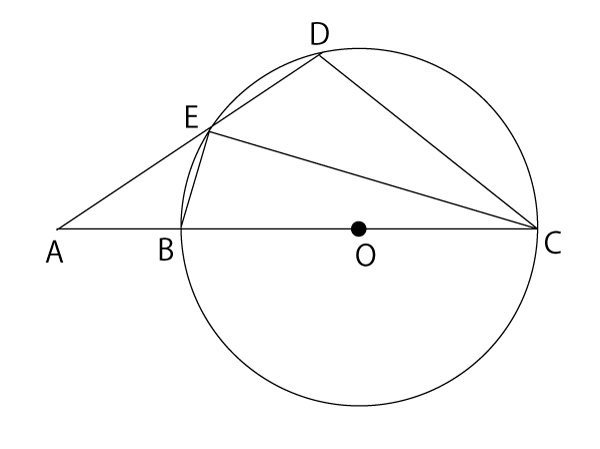
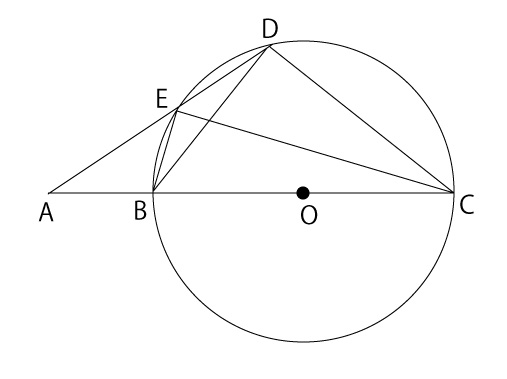
　下の図のように、点Oを中心とする円Oとその外部の点Aがある。直線AOと円Oとの交点のうち、点Aに近い方を点B、もう一方を点Cとする。円Oの円周上に、2点B、Cと異なる手点Dを、線分ADと円Oが点D以外の点でも交わるようにより、その交点を点Eとする。また、点Bと点D、点Bと点E、点Cと点D、点Cと点Eをそれぞれ結ぶ。
このとき、次の（1）～（3）の問いに答えなさい。

（1）次の（a)、（b)に入る最も適当なものを、選択肢のア～エのうちから１つずつ選び、符号で答えなさい。また、（c)に入る最も適当な数を書きなさい。（完答で5点）（正答率80.9%、無答率0.6%)

選択肢　ア∠EBC　イ∠BEC　ウ∠DCB　エ∠BDC

（2）△ABE∽△ADCとなることを証明しなさい。（6点）（正答率（6点）8.7%、部分点（3点）4.0%、(無答率33.8%))
ただし、（1）ののことがらについては、用いてかまわないものとする。

（3）点Eを通る線分ADの垂線と線分ACとの交点を点Fとし、線分EFと線分BDの交点を点Gとする。EG＝1cm、GF＝2cm、∠A＝30°であるとき、線分ABの長さを求めなさい。
（5点）（正答率0%（（無答率）46.9%）)

[next_p]