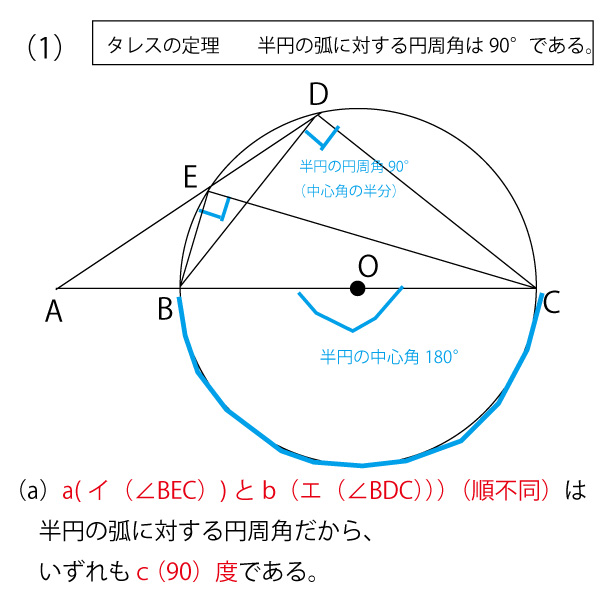
2023年千葉県公立高校入試「数学」第3問（図形の証明）（配点16点）問題・解答・解説
asakura
【解説】
（2）
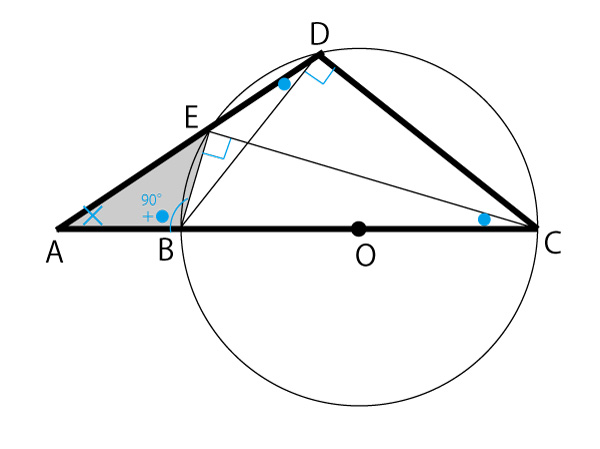
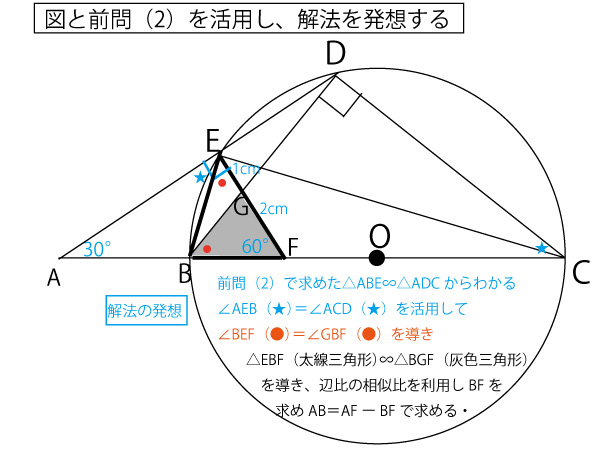
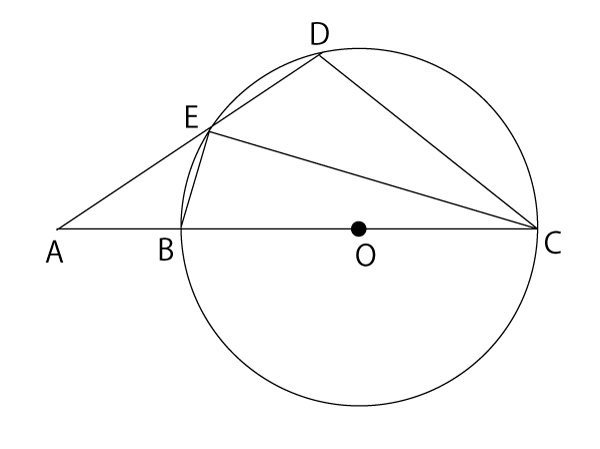
図の灰色三角形△ABEと、図の太線三角形△ADCの相似を証明したい。そして（1）で∠BEC＝∠BDC＝90°を答えたので、それを活用することがヒントとされていると予測する。また「同じ弧に対する円周角は等しい」（円周角の定理）も使うことが予測される。
△ABEと△ADCについて
共通の角なので∠BAE＝∠DAC…
（図×）
直角三角形△BECで、１つの外角は隣り合わない内角の和なので
∠ABE＝∠BEC＋∠ECB＝90°＋∠ECB（図●）‥‥
弧BEに対する円周角は等しいので
∠ECB＝∠EDB（図●）…
∠ADC＝∠BDC＋∠EDB＝90°＋∠EDB…
より、
∠ABE＝∠ADC…
より2組の角がそれぞれ等しいので
△ABE∽△ADC
（（図●）（図×）は説明のための加筆で、入試では解答には書かない。）
中学ではしっかりは学ばないが
「円に内接する四角形の対角の和は180°（円に内接する四角形の１つの内角は対角の外角に等しい）」（後述のまとめ「円周角の性質４」を参照）という定理を用いると以下のように、もっと証明は簡潔になる。
「△ABEと△ADCについて
共通の角なので∠BAE＝∠DAC…
（図×）
四角形BEDCは円に内接している。
円に内接する四角形の対角の和は180°なので、∠ADC＋∠EBC＝180°
∠ADC＝180°ー∠EBC＝∠ABE。
よって、∠ADC＝∠ABE…
。
より2組の角がそれぞれ等しいので△ABE∽△ADC」
ただし、この証明では、（1）の考察を全く使ってないので、この高校入試においては不十分とみなされ、正解とされず部分点（3点）とされる可能性があるので避けたほうがよいだろう。
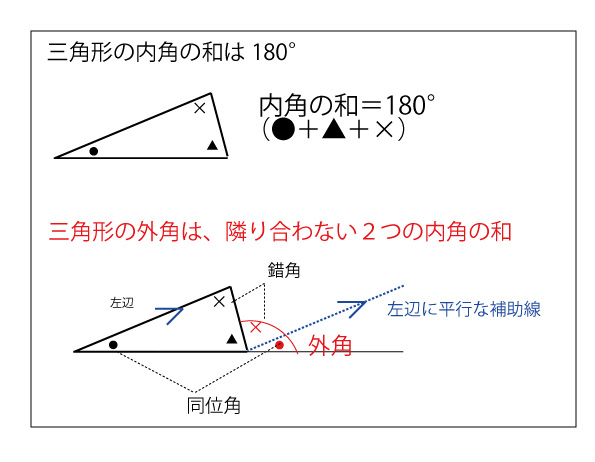
★参考 三角形の内角と外角の関係
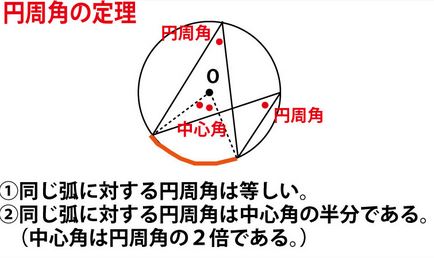
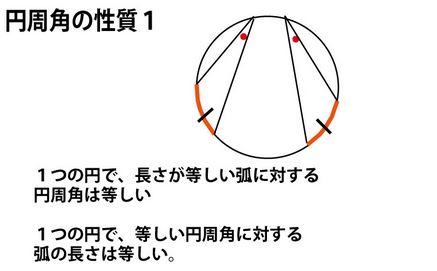
★参考 円周角の定理と円周角の性質１～４
（3）
追記 船橋市教育委員会に対し、千葉県教育委員会に、今回の「図形の証明」第3問（3）の正答率が０％であったことから出題内容が不適切であり、来年以降の出題を改善を求めるように要請します。
千葉県は0.1％単位で正答率を公表しています。毎年、「図形の証明」（3）の問題は正答率は低かったですが、今回の0％は、私がこの解答解説を作成しはじめた2012年以来初めてのことでありきわめて異例です。四捨五入で0.1%になる0.05％以上であれば、正答率０％とはなりませんので、本設問（3）の正答率は0.05%未満だとわかります。0.1％が1000人の1人ですから、2000人に1人も正答できなかったということです。無答率も46.9%で約半数です。2000人の1人未満しか解けない問題は、国民全員が通う権利を保障されている公立中学校の卒業時点の入試問題として不適切で、いたずらに受験生（中3生）を「自分は数学ができない」と落ち込ませるものです。そして学力上位層の選抜にすら貢献していません。あらゆる角度から不適切です。今回の出題を反省し、もう少し問題を標準化することを求めます。
（今年の中３・受験生の皆さんは（3）が解けなくても気にしなくていいです。出題者＝千葉県教育委員会の責任です。ただ、せっかくなので、「解けなくてもいいので」、論理だけは理解しておき、来年の（正答率０％は改善され正答率が若干上がったとしても）「図形の証明」（3）が手強いことは変わらないと思うのでしっかりと勉強しましょう。
拙著「図形の証明」も参考にください。
★参考 拙著「図形の証明」（他３著作）、アマゾンでお求めいただけます。
