2022年大学共通テスト数学ＩＡ第2問[１]問題（15点）・解答・解説

2024年1月13日 2024年1月13日

asakura

2024年1月13日　予備校講師・船橋市議　朝倉幹晴

2022年大学入試共通テスト「数学IA」第2問［１］（配点15点）の解答・解説を作成しましたので、ご活用ください。問題文の最後の所でページ番号「２」をクリックすると解答・解説に飛びます。

2022年大学入試共通テスト数学ⅠA第2問［１］問題（配点15点）・解答・解説

[１]p、qを実数とする。花子さんと太郎さんは、次の二つの2次方程式について考えている。
x²＋px＋q=0・・・・
x²＋qx+p=０・・・・
を満たす実数ｘの個数をｎとおく。
（1)p=4、q=－4のとき、ｎ＝ア（2点）である。
また,p=1、ｑ＝－2のとき、ｎ＝イ（2点）である。
（2)p=－6のとき、ｎ＝３になる場合を考える。
花子：たとえば、をともに満たす実数ｘがあるときはｎ＝３になりそうだね。
太郎：それをαとしたら、α²－6α＋q=0とα²+qa－6＝０が成り立つよ。
花子：なるほど、それならば、α²を消去すれば、αの値が求められそうだね。
太郎：確かにαの値が求まるけど、実際にｎ＝3となっているかどうかの確認が必要だね。
花子：これ以外にもｎ＝３となる場合がありそうだね。
ｎ＝３となるｑの値は、ｑ＝ウ（3点）、エ（2点）である。ただし、ウ＜エとする。

（3）花子さんと太郎さんは、グラフ表示ソフトを用いて、の左辺をｙとおした２次関数ｙ＝x²+px+qとｙ＝x²+qx+pのグラフの動きを考えている。

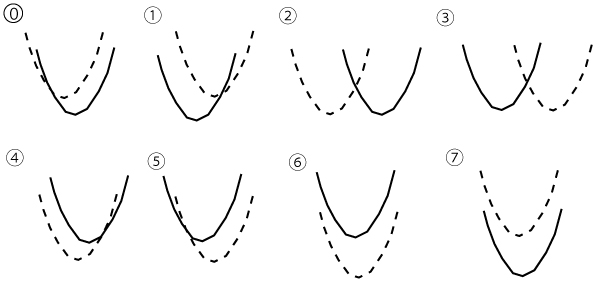
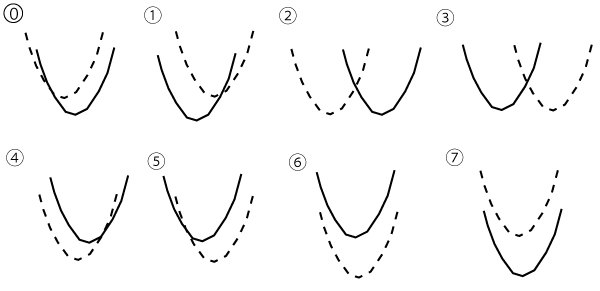
ｐ＝－６に固定したまま、ｑの値だけを変化させる。
ｙ＝x²ー6x＋q・・・・
y=x²+qx－6・・・・
の二つのグラフについて、ｑ＝１のときのグラフを点線で、qの値を１から増加させたときのグラフを実線でそれぞれ表す。
このとき、のグラフの移動の様子を示すとオ（1点）となり、のグラフの移動の様子を示すとカ（2点）となる。
オ、カについては、最も適当なものを、次ののうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。なお、ｘ軸とｙ軸は省略しているが、ｘ軸は右方向、ｙ軸は上方向がそれぞれ正の方向である。

（4）ウ＜ｑ＜エとする。全体集合Ｕを実数全体の集合とし、Ｕの部分集合Ａ、Ｂを
Ａ＝｛ｘ｜ｘ²－6x＋q＜0｝
Ｂ＝｛ｘ｜x²+ｑｘ－6＜０｝
とする。Ｕの部分集合Ｘに対し、Ｘの補集合をと表す。このとき、次のことが成り立つ。
・ｘ∈Aは、ｘ∈Bであるためのキ
・x∈Bは、x∈であるためのク（キク、あわせて3点）