2024年　＃大学入試　＃共通テスト　＃数学１A　第1問［2］（配点20点）問題・解答・解説

［解説］
問１

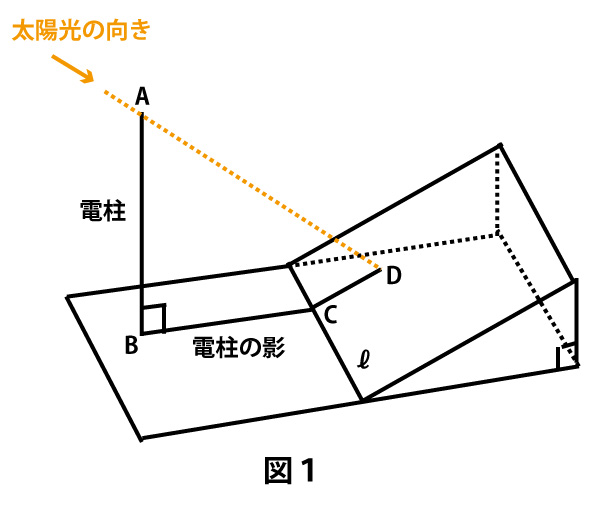
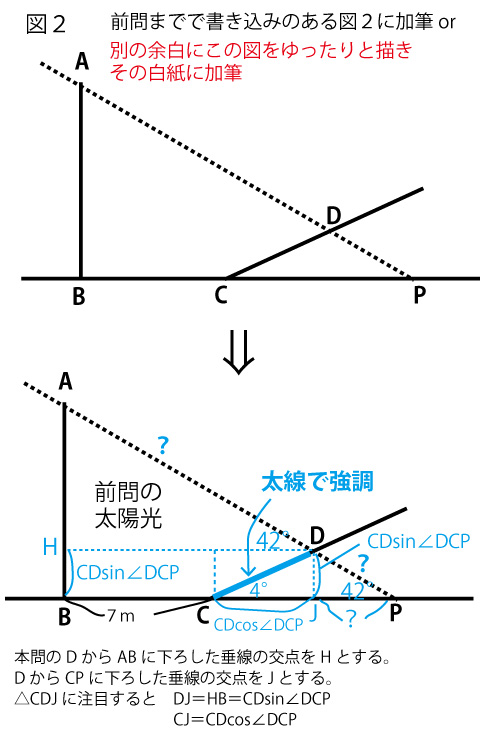
道路標識の7%という表示は、この坂をのぼったとき、100ｍの水平距離に対して7mの割合で高くなることを示している。
つまりtan∠DCP＝７／100＝0.07
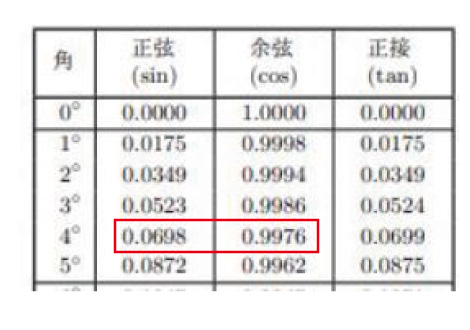
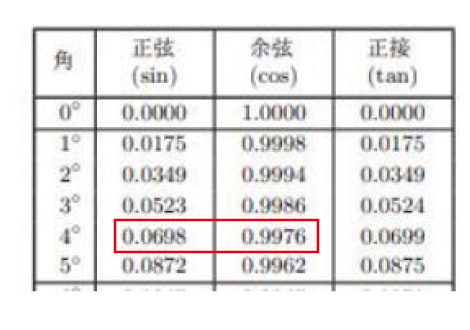
末尾の三角比の表より

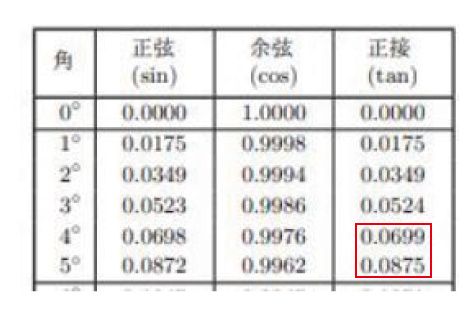
tan4°＜tan∠DCP＜tan(4＋1）°
4°＜∠DCP<４°＋1°
よってn=4（シ答）。

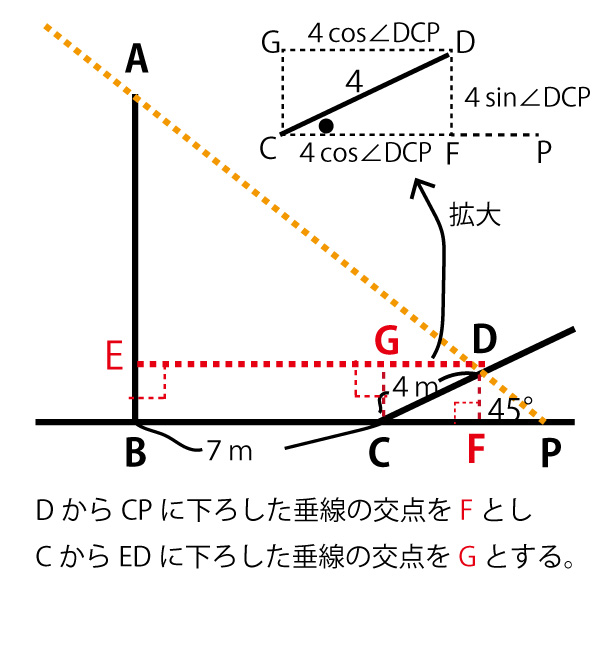
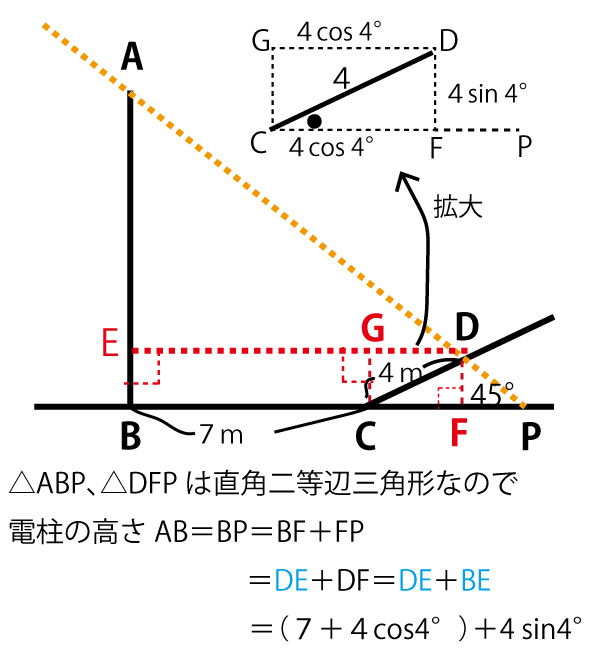
BE=DF
DFは直角三角形CDFの高さとなる。
したがってBE＝DF＝DC×sin∠DCP＝４（ス答）×sin∠DCP（セ答）

DE＝EG＋GD＝BC＋CF＝７＋DC×cos∠DCP
＝7（ソ答）＋4（タ答）×cos∠DCP（チ答）

＝７＋４cos4°＋4sin４°
＝７＋４（cos4°＋sin4°）

＝７＋４×（0.9976＋0.0698 )

＝７＋４×1.0674
（共通テストの限られた時間の中で解くためには、選択肢で選べればよいので、計算時間を節約するため1.0674を1.07として計算しても選べそうである。
≒7＋4×1.07
＝７＋4,28＝11.28=11.3

11.3m
よってツ。