2024年千葉県公立高校入試「数学」第4問（配点18点）問題・解答・解説

2024年9月15日　予備校講師・船橋市議　朝倉幹晴

2024年2月に行われれた千葉県公立高校入試数学第4問（配点18点）の問題・解答・解説を作成しました。普段の学習や2025年2月の千葉県公立高校入試、他県・私立の高校入試対策にお役立てください。なお、千葉県教育委員会が発表した正答率・無答率も付記しました。
ページの最後の[２]をクリックすると解答・解説のページに飛びます。

次の会話文を読み、あとの（1）～（3）の問いに答えなさい。（配点計18点）

会話文
教師T：今日はスクリーンに投影される影について、簡略化したもので考えましょう。
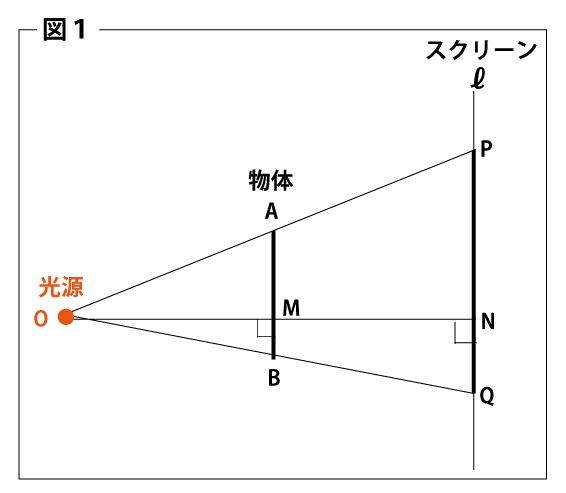
図１のように、光源を点O、スクリーンを直線ℓとし、直線ℓと平行な線分ABを、光源からの光を遮る（さえぎる）物体として考えます。
物体の上端を点A、下端を点Bとし、光源からの光の光の道すじを表したものを、それぞれ半直線OA、OBとします。また、この２つの半直線と直線ℓとの交点を、それをP、Qとします。

生徒X：線分PQがスクリーンに投影された影であると考えればよいのですね。
教師T：そのとおりです。また、点Oから線分PQに垂線をひき、線分ABとの交点をM、線分PQとの交点をNとします。ただし、ここでは必ず交点Mができるように物体ABがあるものとします。
ではOM＝MNのとき、線分PQの長さは線分ABの長さの何倍にありますか。
生徒X：△OABと△OPQは相似になるので、ひ倍です。
生徒T：そうですね。この考え方を利用すると、物体ABが平行移動したとしても、スクリーンに投影される影の長さPQを求めることができますね。
では、線分PQの長さを線分ABの長さの4倍にしたいとき、線分OMと線分MNの長さの比をどのようにすればよいのでしょうか。
生徒X：最も簡単な整数比で表すと、OM：MN＝ふ：へです。
教師T：そのとおりです。次に、光を遮る物体を、線分ではなく正方形としてみましょう。わかりやすくするために、座標平面上で考えてみます。図２のように、光源を表す点Oを原点、物体を表す正方形EFGHの頂点の座標をそれぞれ、E（4,1)、F(4,－1)、G（6,－1)、H（6,1)とし、スクリーンを直線x=10とします。スクリーンに投影される影を線分PQとし、座標をP（10,p)、Q(10,q)とします。ただし、ｐ＞qとします。

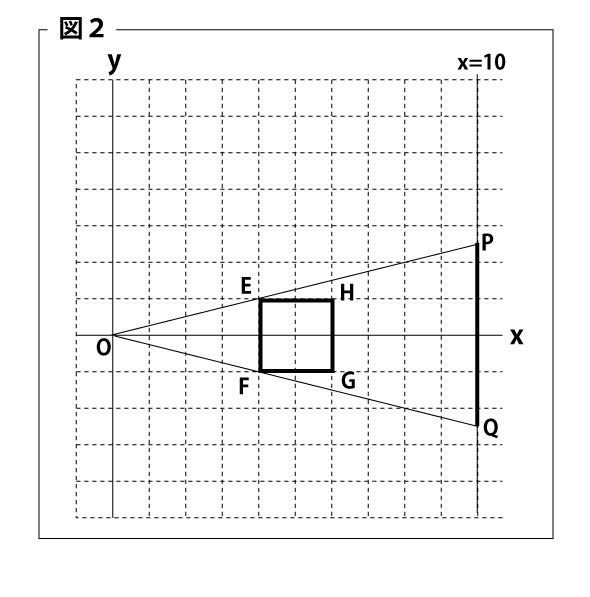
生徒X：点Pは直線OEと直線ｘ＝10との交点だからになるということですね。

教師T：そうですね。では、光源を点Oからｙ軸上の正の整数部分に動かしてみましょう。ｎを自然数とし、動かした後の光源を表す点の座標をO´（0,n)とします。点Pは直線O、Hと直線ｘ＝10との交点、点Ｑは直線Ｏ´Ｆと直線ｘ＝10との交点になるので、点Ｐ、Ｑのｙ座標をそれぞれ求めることができますね。
生徒Ｘ：ｎを用いて表すと、ｐ＝（a)、q=(b)となります。
教師T：正解です。この結果を利用すると、線分PQの長さが周期的に整数になることがわかりますね。

（1）会話文中の「ひ」～「ま」について、次のの問いに答えなさい。

「ひ」にあてはまるものを答えなさい。（3点）（正答率89.7%、無答率2.7%)
「ふ」「へ」にあてはまるものをそれぞれ答えなさい。
           （3点）（正答率33.4%、無答率4.5%)
「ほ」「ま」にあてはまるものをそれぞれ答えなさい。
（3点）（正答率47.6%、無答率19.2%)

（2）会話文中の（a)、（b)にあてはまる式をそれぞれ書きなさい。
（a)(3点）（正答率4.7%、無答率54.9%)   （b)（3点）（正答率5.0%、無答率57.7%)
（3）会話文中の下線部について、次の「み」～「め」にあてはまるものをそれぞれ答えなさい。
線分PQの長さが100cmとなるのは、ｎ＝みむめのときである。
ただし、原点Oから点（1,0)までの距離及び原点Oから点（0,1)までの距離をそれぞれ1cmとする。
  (3点）（正答率3.1％、無答率51.0%)