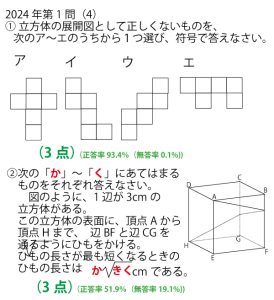
2024年千葉県公立高校入試「数学」第1問（3）問題・解答・解説

2024年第1問（3）解答
イ
（3点）（正答率68.6%、無答率0.1%)
70個

（3点）（正答率70.2%、無答率4.0%)

【解説】

標本調査とは、集団全体の調査対象の数が多く、全てを調査すること（全数調査）が困難であり、一部の標本を取り出して調査することで、集団全体の傾向が把握できる時に行う。

ア（国勢調査）は、日本が5年に1回行い、人口・世帯・年齢構成などを調べるための「全数調査」である。
ウ（学校で行う生徒の歯科検診）やエ（Ａ中学校3年生の進路希望調査）は1人1人全員の歯の健康や進路希望を把握するためのものであり「全数調査」である。

イ（川の水質調査）は、川の水の量は膨大にあるが、その地点の水質の汚染度などを調べるため、数か所の水サンプルをビンなどに採取し、検査して水質調査するので標本調査である。

この方法は、中学（中３）の教科書では、あまり詳しく説明されていない。かし、高校「生物」ではしっかり「標識再捕獲法」という名称で説明されているので本解説でも標識再捕獲法の名称を使った。

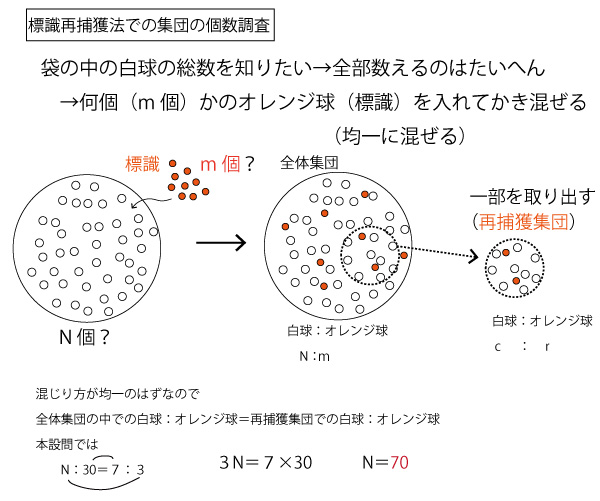
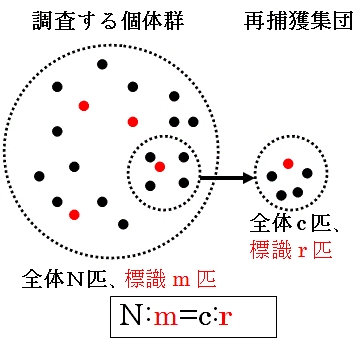
「標識再捕獲法」とは、草原の中でのある動物の総数調査のような場面で使われる。本設問では、オレンジ球を別個に後から加えて、（そのオレンジ球を除いて）もともとあった白球の数を推定させているが、実際の標識再捕獲法では、草原の中の動物を何匹か捕まえて（捕まえる場合も怪我をできるだけしないように配慮）、その動物に標識（その動物行動の影響を与えないような小さなもの）をつけて放し、集団（草原）内で標識個体とその他の個体が自由な位置にまじりあうぐらいの時間を十分経た後、また何匹かを捕獲して（再捕獲）してその再捕獲集団全数とその中の標識個体の比率を知らべる。全体数も標識個体を含めて数え、再捕獲集団の数も標識個体を含めて数えている。（本設問では白球のみを数えているのでその点は異なるが、均一に交わるので比率は同じであるという発想は同じである。）