2025年大学入試共通テスト「数学1A」第4問(配点20点)問題・解答・解説
2025年4月29日 朝倉幹晴(予備校講師・船橋市議)
2025年大学入試共通テスト「数学1A」の第3問(配点20点)の解答解説を作成しました。学習・入試対策にご活用ください。このページを最後までスクロールし、[2]をクリックすると、解答・解説のページに飛びます。
解説の動画も作ったのでご覧ください。
2025年大学入試共通テスト「数学1A」第4問(配点20点)
ある行事で、主催者が次のゲームを計画している。
ゲーム
参加者はくじを最大3回引き、当たりが出たら、1200円相当の景品を主催者から受け取り、以降はくじを引かない。参加者はくじを1回目、2回目、3回目で異なる線から引く。1回目のくじ引きで当たりが出なかった場合は2回目のくじを引き、2回目のくじ引きでも当たりが出なかった場合は3回目のくじを引く。主催者は、当たりの出る確率について次のとおり設定する。
・1回目に当たりが出る確率は![]() である。
である。
・1回目に当たりが出ず、かつ2回目に当たりが出る確率は![]() である。
である。
・1回目、2回目ともに当たりが出ず、かつ3回目に当たりが出る確率は![]() である。
である。
ゲームの参加料について、主催者は2種類の支払い方法を考えている。参加料に関する設定の妥当性について、主催者は判断を行う。
以下では、主催者が参加者に対して負担する金額をX円とする。すなわち、参加者がゲームで景品を受け取るときX=1200、参加者がゲームで景品を受け取らないときX=0である。
(2)
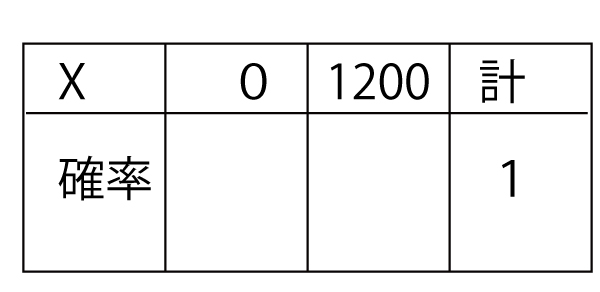
(i)数量Xの期待値はコサシ(3点)である。なお、必要に応じて、次に示す表を用いて考えてもよい。

(ii)次の支払い方法1を考える。
支払い方法1
参加者は1回目のくじを引く直前に参加料500円を支払う。
支払い方法1の場合、主催者が負担する金額X円の期待値が、参加料の金額500円以上であるとき、参加料の設定は妥当ではないと判断する。
(i)で求めたX円の期待値コサシ円は参加料の金額500円ス。したがって、主催者は参加料500円という設定についてセと判断する。
(スセで合わせて1点)
(3)aを正の整数とする。次の支払い方法2を考える。
支払い方法2
参加者は1回目、2回目、3回目のくじを引く直前にそれぞれ料金a円を支払う。なお、この料金をくじ引き料といい、当たりが出た後は、くじを引かないため、くじ引き料を支払わないこととなる。
支払い方法2で、ゲームを通して参加者が支払うっくじ引き料の合計を参加料とし、Y円で表す。
(i)a=170とする。このとき、次が成り立つ。
・1回目に当たりが出るとき、Y=170である。
・1回目に当たりが出ず、かつ2回目に当たりが出るとき、Y=340である。
・1回目、2回目ともに当たりがでないとき、Y=510である。
数量Yの期待値はソタチ(3点)である。なお、必要に応じて、次に示す表を用いて考えてもよい。
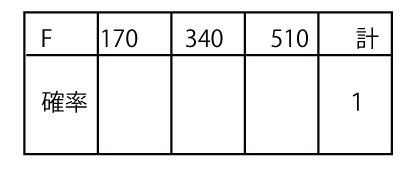
(ii)支払い方法2の場合、主催者が負担する金額X円の期待値が、参加料Y円の期待値未満であるとき、主催者はくじ引き料の設定は妥当ではないと判断する。
(2)の(i)で求めたX円の期待値コサシ円は、a=179と設定した場合の支払い方法2で参加者が支払う参加料Y円の期待値ソタチ(3点)円ツ。
したがって、主催者はくじ引き料170円という設定についてテと判断する。(ツテあわせて1点)
また、主催者がくじ引き料の設定が妥当であると判断するのは、a>トナニ(3点)のときであり、主催者がくじ引き料の設定が妥当ではないと判断するのはa≧トナニのときである。