2025年大学入試共通テスト「数学1A」第3問（配点20点）問題・解答・解説

2025年4月29日　朝倉幹晴（予備校講師・船橋市議）
2025年大学入試共通テスト「数学1A」の第3問（配点20点）の解答解説を作成しました。学習・入試対策にご活用ください。このページを最後までスクロールし、[２]をクリックすると、解答・解説のページに飛びます。

2025年大学入試共通テスト「数学1A」第3問（配点20点）

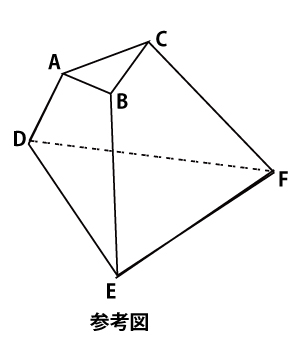
６点A、B、C、D、E、Fを頂点とし、三角形ABCとDEF、および四角形ABED、ACFD、BCFEを面とする五面体がある。ただし、直線ADとBEは平行でないとする。
以下では、例えば、面ABCを含む平面を平面ABC、面ABEDを含む平面を平面ABED、などということにする。

（1）３直線AD、BE、CFは1点で交わる。これを証明しよう。
直線ADとBEは平面ABED上にあり、平行でないので1点で交わる。その交点をPとする。
点Pは直線AD上にあり、直線ADは平面ABEDと平面アとの交線であるから、点Ｐは平面ア上にあることがわかる。
また、点Pは直線BE上にあり、直線BEは平面ABEDと平面イとの交線であるから、点Pと平面イ上にあることがわかる。
平面アと平面イとの交線は直線CFであるから、点Pは直線CF上にあることがわかる。したがって、３直線AD、BE、CFは点Pで交わる。（アイあわせて2点）

（2）五面体において、面ABCは一辺の長さが３の正三角形であり

AD＝７、BE＝11、CF＝17、DE＝９
であるとする。また、6点A、B、C、D、E、Fはある一つの球面上にあるとし、その球面をSとする。直線ADとBEの交点をPとする。

（i）平面ABEDと球面Sが交わる部分は円であり、4点A、B、E、Dはその円周上にある。このことから、三角形PABとPEDは相似であることがわかり、その相似比は１：ウである。したがって
ウPA＝PB＋エオ
ウPB＝PA＋カ　　（ウ3点、エオカあわせて2点）
が成り立つ。よって
PA＝キ、PB＝ク　（キク3点）
となる。

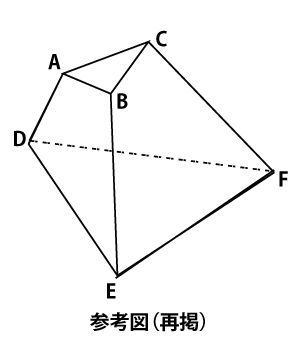
（ii)平面BCFEと球面Sが交わる部分に着目すると、方べきの定理より

PC＝ケ（3点）
となる。したがって
EF＝コサ、DF＝シス　（コサシスであわせて3点）

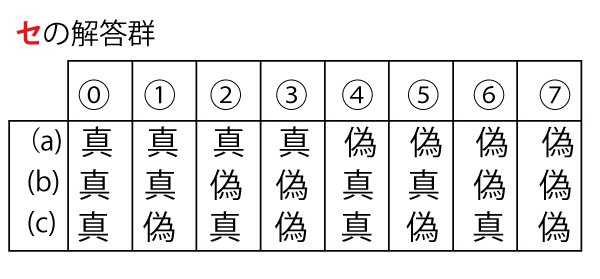
（iii)∠ADE、∠ADF、∠EDFの大きさに着目すると、次の命題（a)、（b)、（c)の真偽の組合せとして正しいものはセ（4点）であることがわかる。

（a)平面ABEDと平面DEFは垂直である。
（b)直線DEは平面ACFDに垂直である。
（c)直線ACと直線DEは垂直である。