2025年大学入試共通テスト「数学1A」第3問(配点20点)問題・解答・解説
(1)
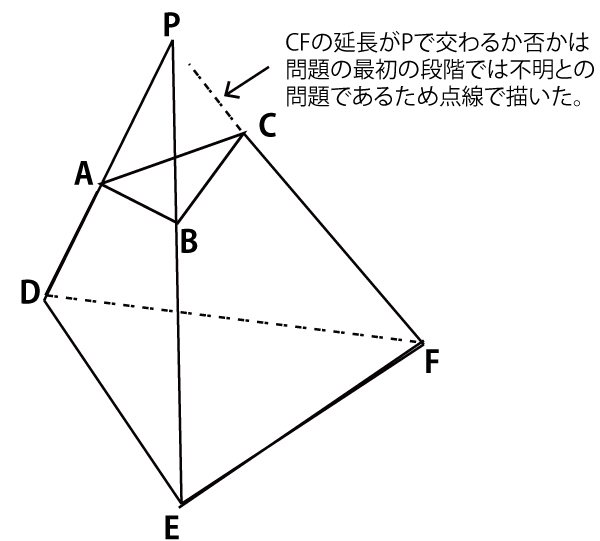
3直線AD、BE、CFは1点で交わる。これを証明しよう。
直線ADとBEは平面ABED上にあり、平行でないので1点で交わる。その交点をPとする。
点Pは直線AD上にあり、直線ADは平面ABEDと平面ア(ACFD・答![]() )との交線であるから、点Pは平面ア(ACFD)上にあることがわかる。
)との交線であるから、点Pは平面ア(ACFD)上にあることがわかる。
また、点Pは直線BE上にあり、直線BEは平面ABEDと平面イ(BCFE・答![]() )との交線であるから、点Pと平面イ(BCFE)上にあることがわかる。
)との交線であるから、点Pと平面イ(BCFE)上にあることがわかる。
平面ア(ACFD)と平面イ(BCFE)との交線は直線CFであるから、点Pは直線CF上にあることがわかる。
したがって、3直線AD、BE、CFは点Pで交わる。(アイあわせて2点)
直観的にはこれは「三角すいを上部を斜めにスパッと切り落した図形」であり、それぞれの斜辺はもともとの三角すいの頂点Pで交わるのは自明のように感じる。しかし、幾何学の祖で、アレクサンドリアで研究を進めたエウクレイデス(ユークリッド)はその「原論」の中で、自明と思えることでも、最初から丁寧に証明していく形で論を進めた。この問題はエウクレイデスの原点を思い返される問題である。
(2)
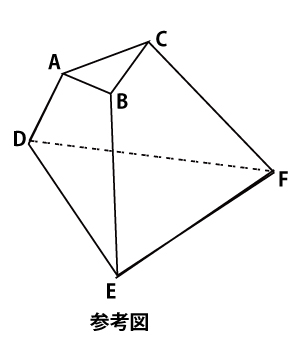
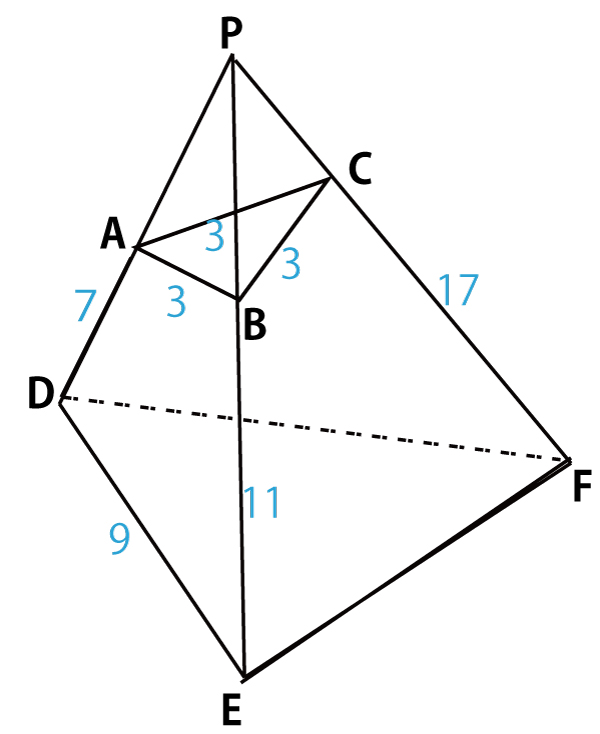
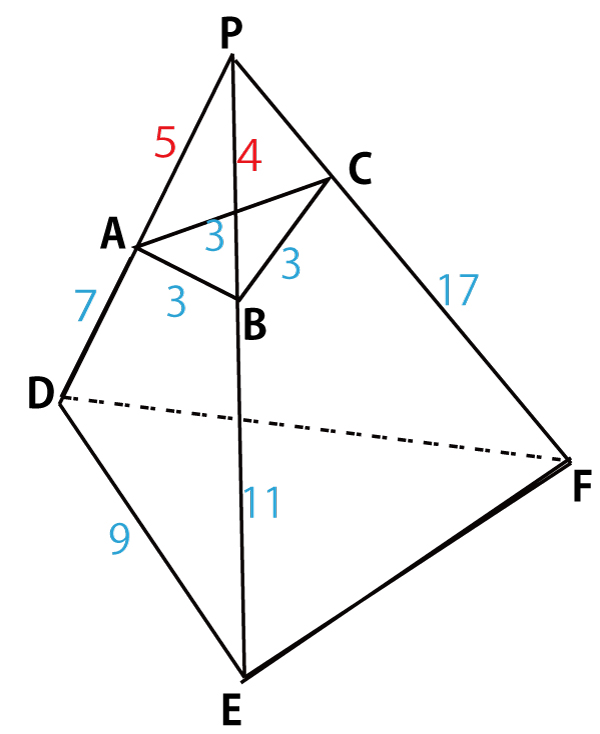
五面体において、面ABCは一辺の長さが3の正三角形であり
AD=7、BE=11、CF=17、DE=9
であるとする。また、6点A、B、C、D、E、Fはある一つの球面上にあるとし、その球面をSとする。直線ADとBEの交点をPとする。
(i)平面ABEDと球面Sが交わる部分は円であり、4点A、B、E、Dはその円周上にある。
円に内接する四角形では、ある内角とその対角の外角は等しい。以下の図にように、∠BED=∠PAB(●)。
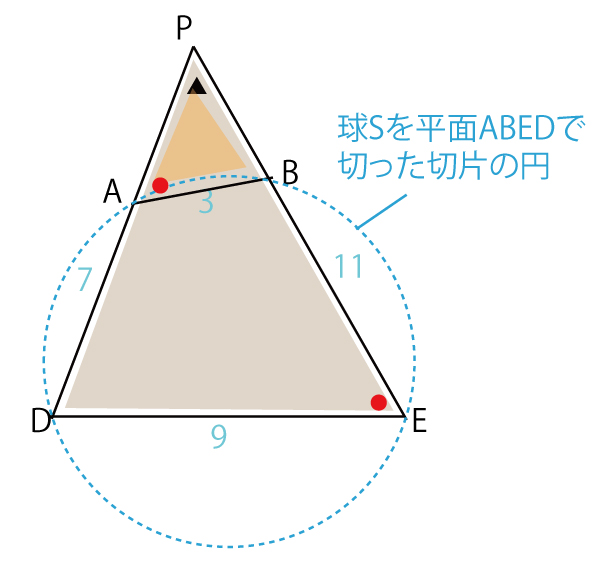
△PABと△PEDにおいて、∠PAB=∠PED(▲)、∠BED=∠PAB(●)で2つの角がそれぞれ等しいので、△PAB∽△PED。
このことから、三角形PABとPEDは相似であることがわかる。
対応する辺で、AB:ED=3:9=1:3。
り、その相似比は1:ウ(3)である。
ウ(3)PA、ウ(3)PBは、PA、PBに対応する△PEDの辺のPE、PD。
よって
ウ(3)PA=PE=PB+BE=PB+11(エオ答)
ウ(3)PB=PD=PA+AD=PA+7(カ答)
が成り立つ。よって
3PA=PB+11
PB=3PA-11・・・![]()
3PB=PA+7
PA=3PB-7・・・![]()
PA=9PA-33−7
-8PA=-40
PA=5(キ答)
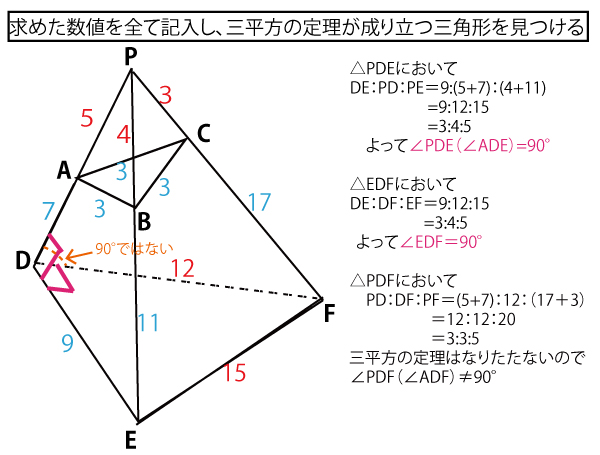
わかった値を図に書き込むと以下のようになる。
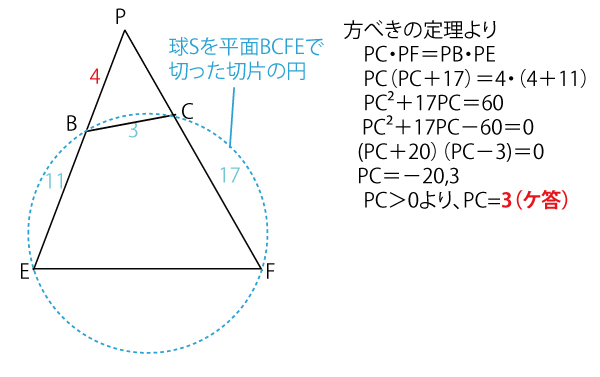
(ii)
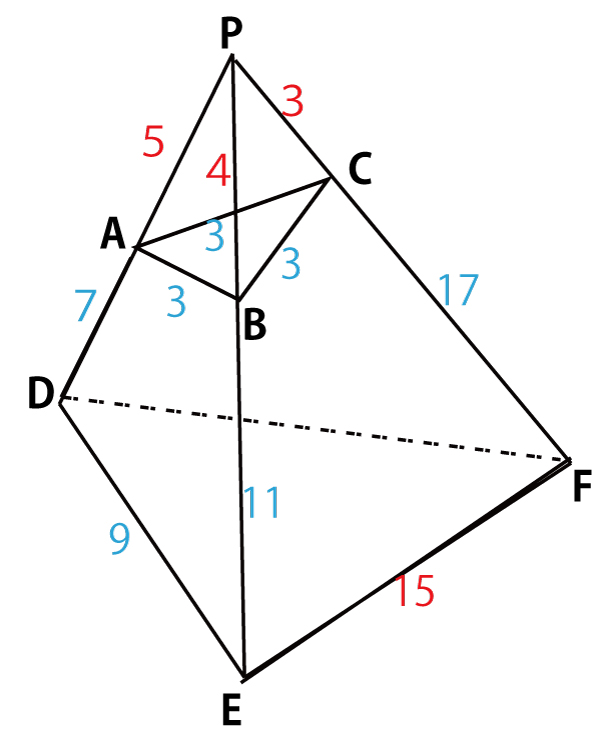
これまで求めた数値を図に書き込むと以下のようになる。
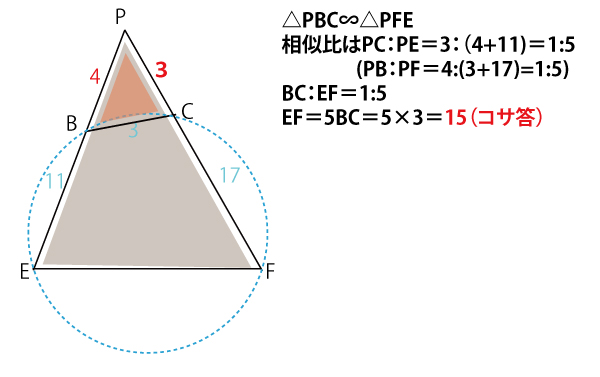
図の奥の面に関して、これまで同様に、△PAC∽△PFD
相似比はPA:PF=5:3+17=5:20=1:4
(あるいはPC:PD=3:5+7=3:12=1:4)
よってAC:FD=1:4 AC=3なので 3:ED=1:4
FD=12(シス答)
(a)平面ABEDと平面DEFは垂直である。 偽
図のオレンジで示したように垂直ではない。
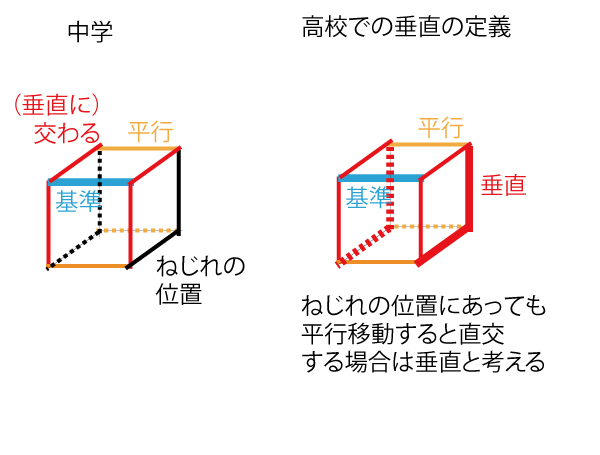
(b)直線DEは平面ACFDに垂直である。真
(c)直線ACと直線DEは垂直である。 真 (ACは平面ACFDに含まれている。したがって平行移動すると直交するので垂直である。)