2025年千葉県公立高校入試「数学」第1問（5）問題・解答・解説（計6点）

2026年1月6日 2026年1月6日

asakura

2026年1月6日（火）　　船橋市議（無党派）・予備校講師　朝倉幹晴

2025年2月に行われれた千葉県公立高校入試数学第1問（5）（確率、配点６点）の問題・解答・解説を作成しました。普段の学習や2026年2月の千葉県公立高校入試、他県・私立の高校入試対策にお役立てください。なお、千葉県教育委員会が発表した正答率・無答率も付記しました。

問題ページの最後で「２」をクリックすると解答・解説のページに飛びます。

第1問（5）（計6点）

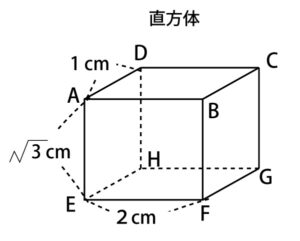
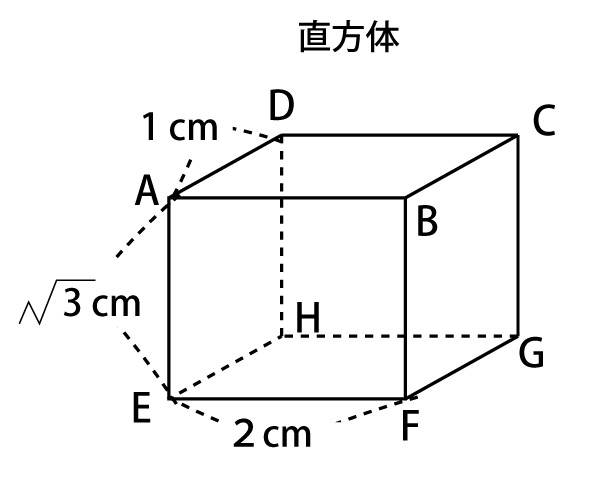
図のように、の直方体と、A、B、C、D、E、F、G、Hの文字が１つずつ書かれた8枚のカードがある。

この8枚のカードをよくきって、同時に2枚のカードをひく。ひいたカードに書かれた文字と直方体の頂点の文字は対応しているものとし、ひいたカードに書かれた２つの文字の頂点を結んでできる線分について考える。例えば、AとBの文字が書かれたカードを同時にひいた場合は、線分ABについて考える。
このとき、次のの「か」「き」、の「く」「け」にあてはまるものをそれぞれ答えなさい。ただし、どのカードをひくことも同様に確からしいものとする。