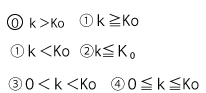大学入試共通テスト2022年数ⅡB第1問[1](図形と方程式・配点15点)問題、解答、解説
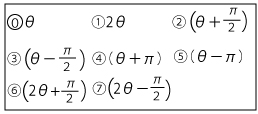
2022年6月 予備校講師・船橋市議(無党派) 朝倉幹晴
大学入試共通テスト2022年の数ⅡB第1問[1](図形と方程式・配点15点)の解答、解説を作りましたので、勉強、入試対策のご活用ください。第1問[2]は対数で別内容なので解答・解説は後日、別に作成します。
大学入試共通テスト2022年の数ⅡB第1問[1](配点15点)
座標平面上に点A(-8,0)をとる。また、不等式
x2+y2−4xー10y+4≦0
の表す領域をDとする。
(1)領域Dは、中心が点(ア,イ)、半径がウの円のエである。
以下、点(ア,イ)をQとし、方程式
x2+y2−4xー10y+4=0
の表す図形をCとする。
(2)点Aを通る直線と領域Dが共有点をもつのはどのようなときかを考えよう。
(i)(1)により、直線y=オは点Aを通るCの接線の一つとなることがわかる。
太郎さんと花子さんは点Aを通るCのもう一つの接線について話している。
点Aを通り、傾きがkの直線をℓとする。
太郎:直線ℓの方程式はy=k(x+8)と表すことができるから、
これを
x2+y2−4xー10y+4=0
に代入することで接線を求められそうだね。
花子:x軸と直線AQのなす角のタンジェントに着目することでも求められそうだよ。
(ⅱ)太郎さんの求め方について考えてみよう。
y=k(x+8)をx2+y2−4xー10y+4=0に代入すると、xについての2次方程式
(k2+1)x2+(16k2−10k-4)x+64k2ー80k+4=0
が得られる。この方程式がカのときのkの値が接線の傾きとなる。
カの解答群
(ⅲ)花子さんの求め方について考えてみよう。
x軸と直線AQのなす角をθ(0<θ≦![]() )とすると
)とすると

であり、直線y=オと異なる接線の傾きはtanケ(2点)と表すことができる。
と異なる接線の傾きをkoとする。このとき、(ⅱ)または(ⅲ)の考え方を用いることにより
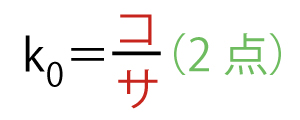
であることがわかる。
直線ℓと領域Dが共有点をもつようなkの値の範囲はシ(2点)である。
シの解答群