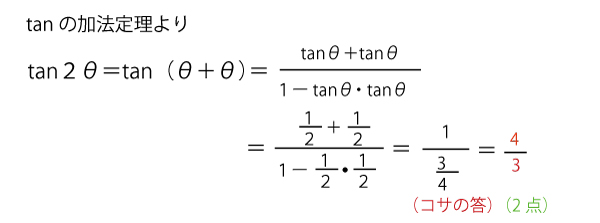大学入試共通テスト2022年数ⅡB第1問［１］（図形と方程式・配点15点）問題、解答、解説

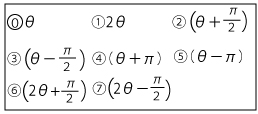
解説

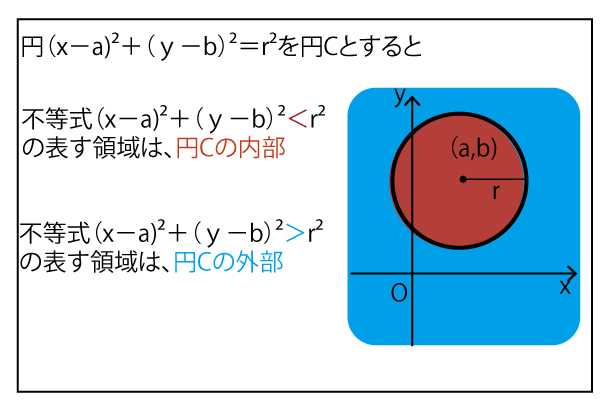
（1）x²＋y²−4xー10ｙ＋４≦０
x²−4x＋４＋y²ー10ｙ≦０
x²−4x＋４＋y²ー10ｙ＋25≦25
（ｘ－2)²＋（ｙー5）²≦5²  。したがって、中心(2,5)、半径5の円の周、および内部（）（ア～エの答）

（2）（i）

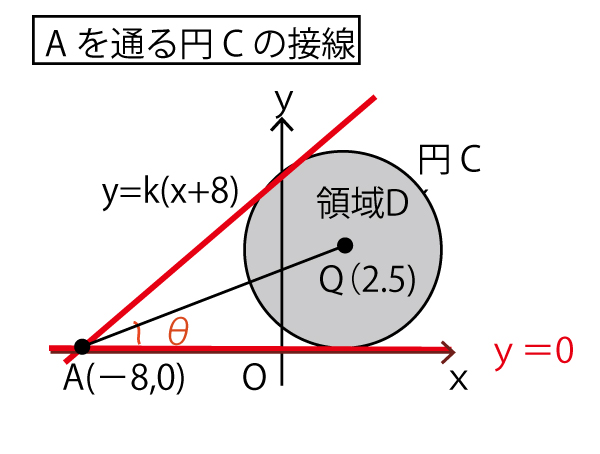
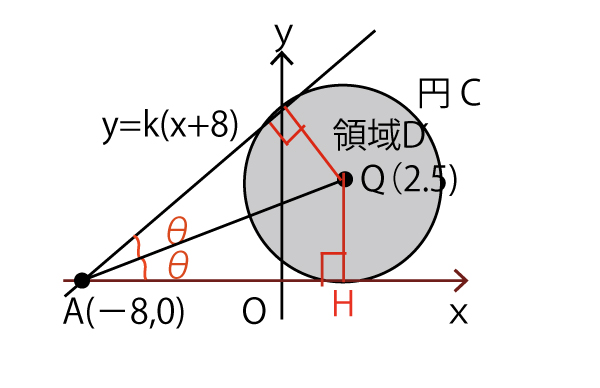
Aを通り円Cに接する接線の一つはｘ軸で、ｙ＝０（オの答）
もう一つの接線は（－8、0）を通り傾きKの直線なので
ｙ－０＝ｋ（ｘー（－8））
ｙ＝ｋ（ｘ＋８）

（ⅱ）ｙ＝k(x+8)をx²＋y²−4xー10ｙ＋４＝0に代入すると、ｘについての2次方程式
（k²＋1）x²＋（16k²−10k－4)x＋64k²ー80k＋4＝０
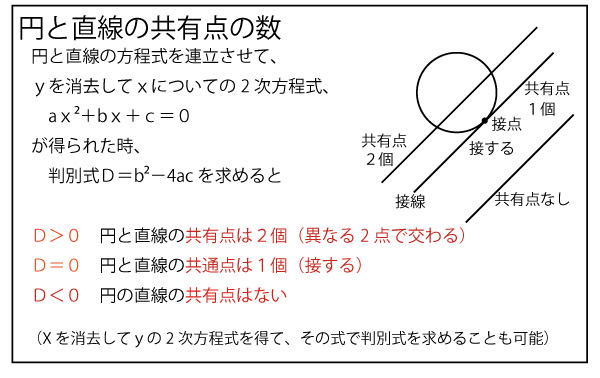
これが重解を持つ（カの答）ときのｋの値が接線の傾きとなる。

（ⅲ）
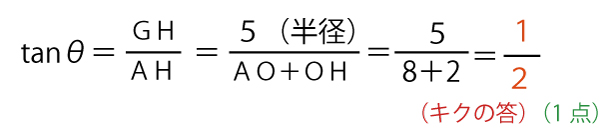
Qからｘ軸（ｙ＝０）に下ろした垂線の交点をＨとすると

ｙ＝０と異なる接線の傾きはtan2θ（ケの答、）

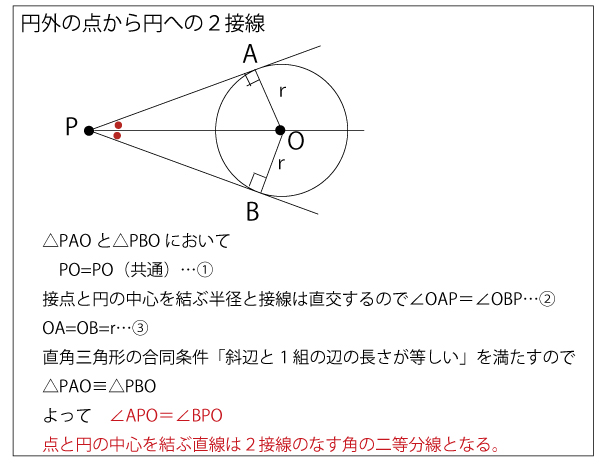
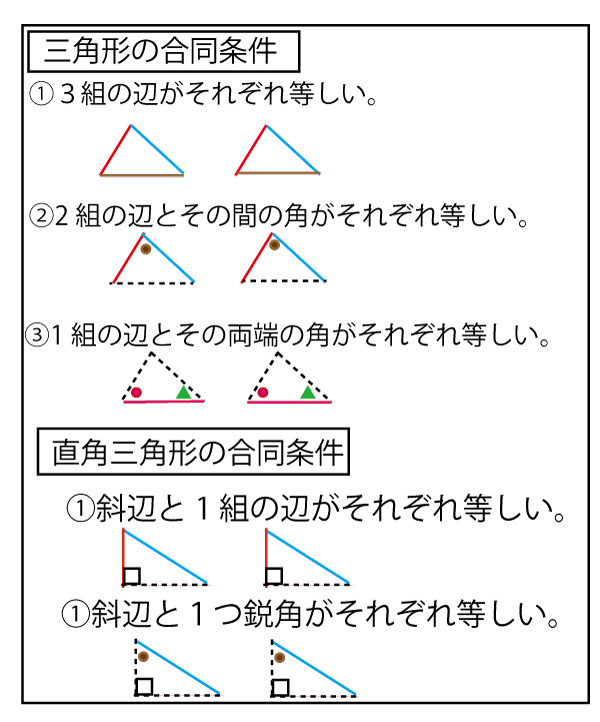
＜参考、上記証明で使っている三角形・直角三角形の合同条件の復習です＞

（ⅳ）

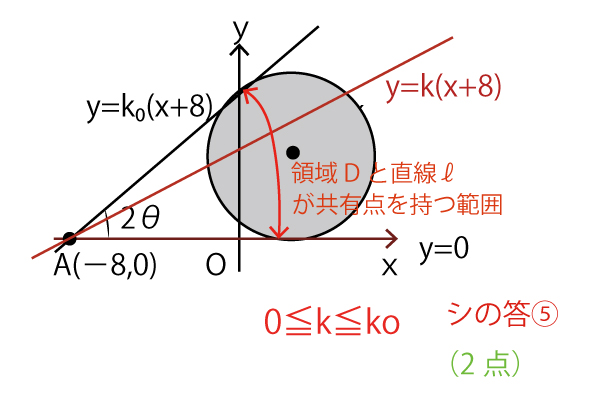
点Aを通るCの接線のうち、直線y＝0と異なる接線の傾きをｋ_oとする。
傾きK₀の直線（接線）とｘ軸のなす角は２θであり、傾きＫ_oはtan２θである。