2021年共通テスト数学ⅠA(第2日程)第5問(図形)(計20点)問題・解答・解説
2022年6月 予備校講師・船橋市議(無党派) 朝倉幹晴
2021年共通テスト数学ⅠA(第2日程)第5問(図形)(計20点)の解答・解説を作成しました。学習、入試対策にご活用ください。
(解答・解説は末尾をクリックすると次のページにあります)
2021年共通テスト数学ⅠA(第2日程)第5問(図形)(計20点)
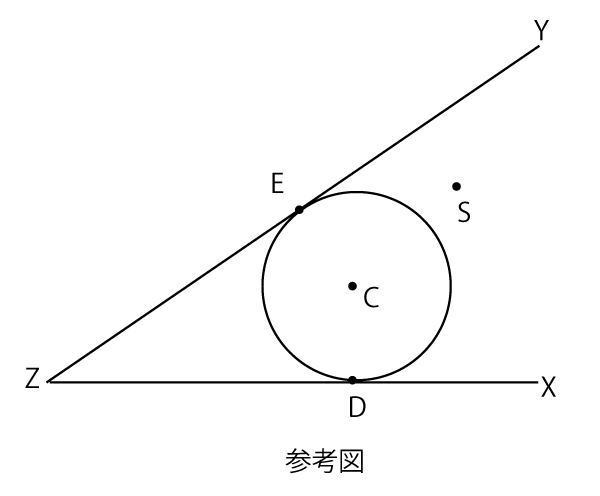
点Zを端点とする半直線ZXと半直線ZYがあり、0°<∠XZY<90°とする。また、0°<∠SZX<∠XZYを満たす点Sをとる。
++点Sを通り、半直線ZXと半直線ZYの両方に接する円を作図したい。
円Oを、次の(Step1)~(Step5)の手順で作図する。
手順
(Step1)∠XZYの二等分線ℓ上に点Cをとり、下図のように半直線ZXと半直線ZYの両方に接する円Cを作図する。
また、円Cと半直線ZXとの接点をD、半直線ZYとの接点をEとする。
(Step2)円Cと直線ZSとの交点の一つをGとする。
(Step3)半直線ZX上に点Hをを満たすようにとる。
(Step4)点Hを通り、半直線ZXに垂直な直線を引き、ℓとの交点をOとする。
(Step5)点Oを中心とする半径OHの円Oをかく。
(1)(Step1)~(Step5)の手順で作図した円Oが求める円であることは、次の構想に基づいて下のように説明できる。
構想
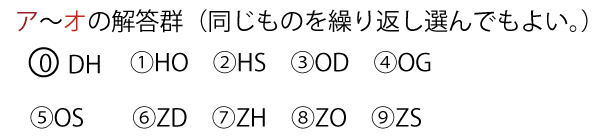
円Oが点Sを通り、半直線ZXと半直線ZYの両方に接する円であることを示すには、OH=ア(2点)が成り立つことを示せばよい。
作図の手順より、△ZDGと△ZHSとの関係、および△ZDCと△ZHOとの関係に着目すると
DG:イ=ウ:エ(合わせて2点)
DC:オ=ウ:エ(オ1点)
であるから、DG:イ=DC:オとなる。
ここで、3点S、G、Hが一直線上にない場合は、∠CDG=∠カ(2点)であるので、
△CDGと△カとの関係に着目すると、CD=CGよりOH=アであることがわかる。
なお、3点S、O、Hが一直線上にある場合は、DG=キDC(キ1点)となり、DG:イ=DC:オよりOH=アであることがわかる。
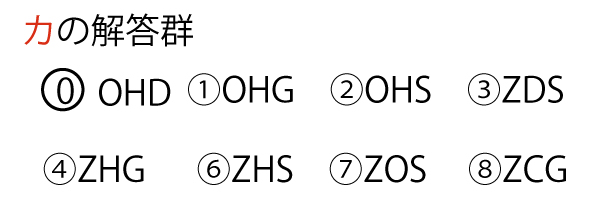
(2)点Sを通り、半直線ZXと半直線ZYの両方に接する円は二つ作図できる。
特に、点Sが∠XZYの二等分線ℓ上にある場合を考える。半径が大きい方の円の中心をO1とし、
半径が小さい方の円の中心をO2とする。また円O2と半直線ZYが接する点をIとする。
円O1と半直線ZYが接する点をJとし、円O1と半直線ZXが接する点をKとする。
作図をした結果、円O1の半径は5、円O2の半径は3であったとする。
このとき、![]() である。さらに、円O1と円O2の接点Sにおける
である。さらに、円O1と円O2の接点Sにおける
共通接線と半直線ZYとの交点をLとし、直線LKと円O1との交点で点Kとは異なる点をMとすると
LM・LK=サシ(3点)
である。
また、![]() であるので、直線LKと直線ℓとの交点をNとすると
であるので、直線LKと直線ℓとの交点をNとすると
である。
[next_p]