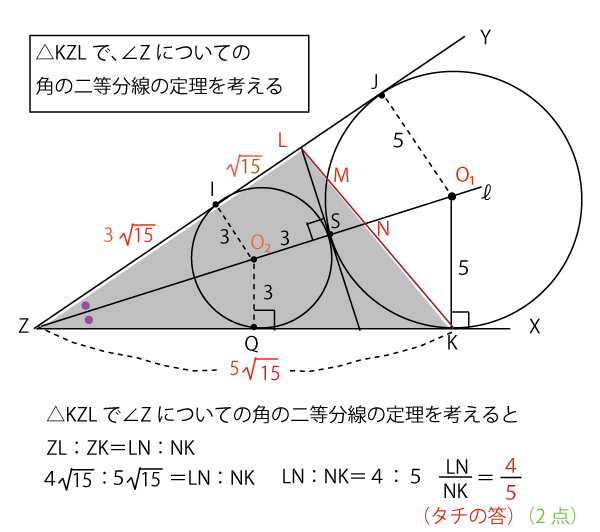
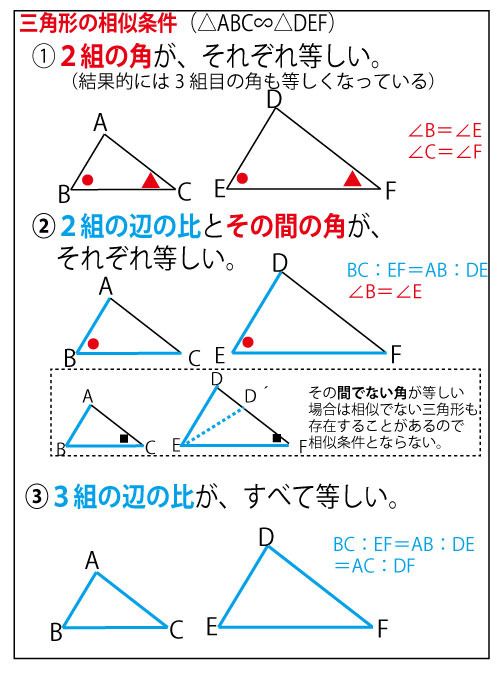
2021年共通テスト数学ⅠA(第2日程)第5問(図形)(計20点)問題・解答・解説
解説
手順
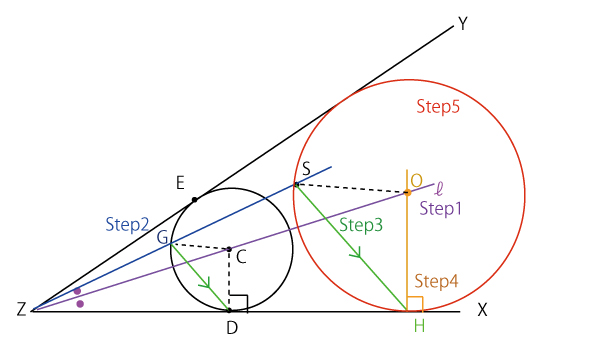
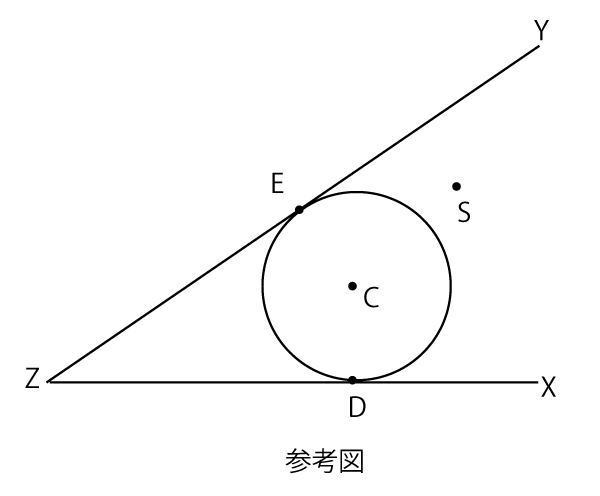
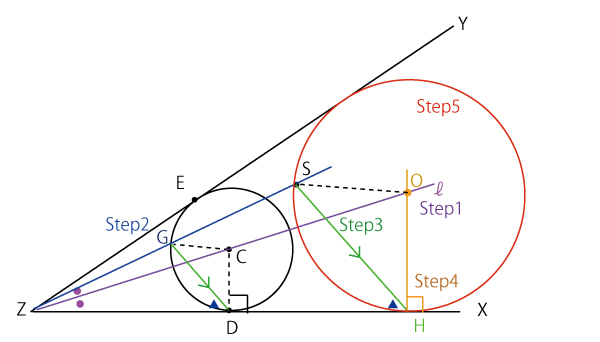
(Step1)∠XZYの二等分線ℓ上に点Cをとり、下図のように半直線ZXと半直線ZYの両方に接する円Cを作図する。また、円Cと半直線ZXとの接点をD、半直線ZYとの接点をEとする。
(Step2)円Cと直線ZSとの交点の一つをGとする。
(Step3)半直線ZX上に点Hを![]() を満たすようにとる。
を満たすようにとる。
(Step4)点Hを通り、半直線ZXに垂直な直線を引き、ℓとの交点をOとする。
(Step5)点Oを中心とする半径OHの円Oをかく。
で作図すると以下のようになる。(なお図中の点線はStep5まででは作図されないが、その後の設問を解くときに必要な補助線なのであらかじめ加筆した。)
△ZDGと
△ZDGと△ZHSについて
![]() でZXとなす角で同位角なので
でZXとなす角で同位角なので
∠ZDG=∠ZHS…![]()
∠DZG=∠HZS(共通)…![]()
![]()
![]() より2組の角がそれぞれ等しく
より2組の角がそれぞれ等しく
△ZDG∽△ZHSなので
相似比から
DG:HS(イの答![]() )=ZD(ウの答
)=ZD(ウの答![]() ):ZH(エの答
):ZH(エの答![]() )(あわせて2点)
)(あわせて2点)
△ZDCと△ZHOについて
∠ZDC=∠ZHO=90°…![]()
∠DZC=∠HZO(共通)…![]()
![]()
![]() より2組の角がそれぞれ等しく
より2組の角がそれぞれ等しく
△ZDS∽△ZHOなので
相似比から
DC:HO(オの答![]() )=ZD:ZH(オ2点)
)=ZD:ZH(オ2点)
ここで、3点S、O、Hが一直線上にない場合は、
∠CDGと∠OHSに注目すると
∠CDG=∠ZDC(90°)ー∠ZDG…![]()
∠OHS=∠ZHO(90°)ー∠ZHS…![]()
![]()
![]()
![]() より
より
∠CDG=∠OHS(カの答![]() )(2点)…
)(2点)…![]()
である。
△CDGと△OHSについて
![]()
![]() より
より
2組の辺の比とその間の角が等しいので
△CDG∽△OHSなので、CDとCGは円Cの半径でCD=CGより、
相似の三角形の辺比は等しいのでOH=OS(ア)であることがわかる。
<参考>(中学の復習)
S,O,Hが一直線上にある場合、円がZXに接することは変わらないのでOH⊥ZHより、
SはZXに対する垂線上にある。
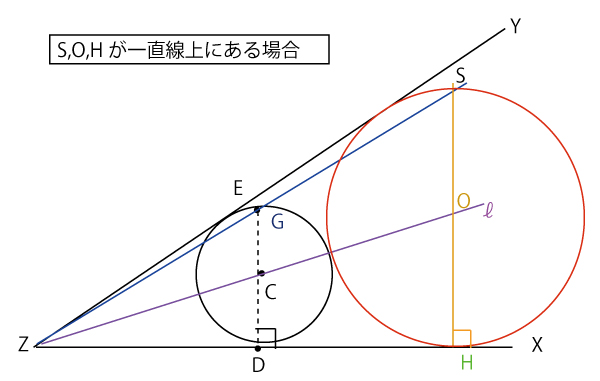
すると![]() なので、GもZXに対する垂線上にあり、円Cの直径と半径に相当するので
なので、GもZXに対する垂線上にあり、円Cの直径と半径に相当するので
DG=2(キの答)DC (2点)
点Sを通り、半直線ZXと半直線ZYの両方に接する円は二つ作図できる。
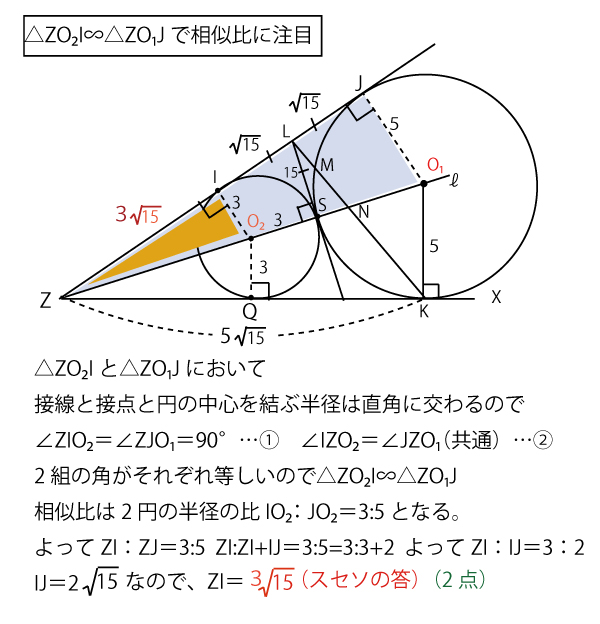
特に、点Sが∠XZYの二等分線ℓ上にある場合を考える。半径が大きい方の円の中心をO1とし、
半径が小さい方の円の中心をO2とする。また円O2と半直線ZYが接する点をIとする。
円O1と半直線ZYが接する点をJとし、円O1と半直線ZXが接する点をKとする。
作図をした結果、円O1の半径は5、円O2の半径は3であったとする。
ここまでを作図すると以下になる。
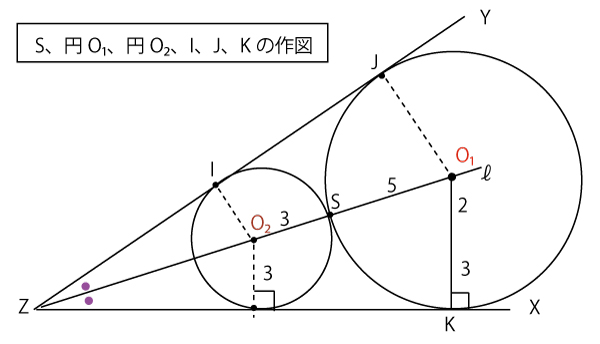
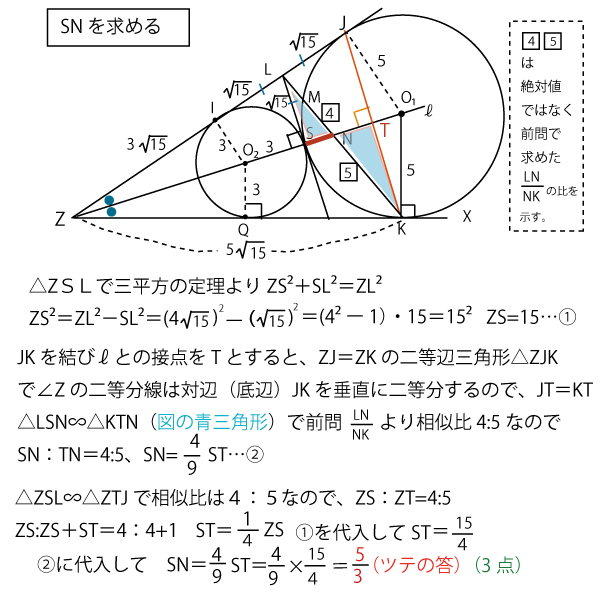
これからIJの長さを求めるために、直角三角形を考えて三平方の定理を使ってみる。
さらに、円O1と円O2の接点Sにおける
共通接線と半直線ZYとの交点をLとし、
直線LKと円O1との交点で点Kとは異なる点をMとすると
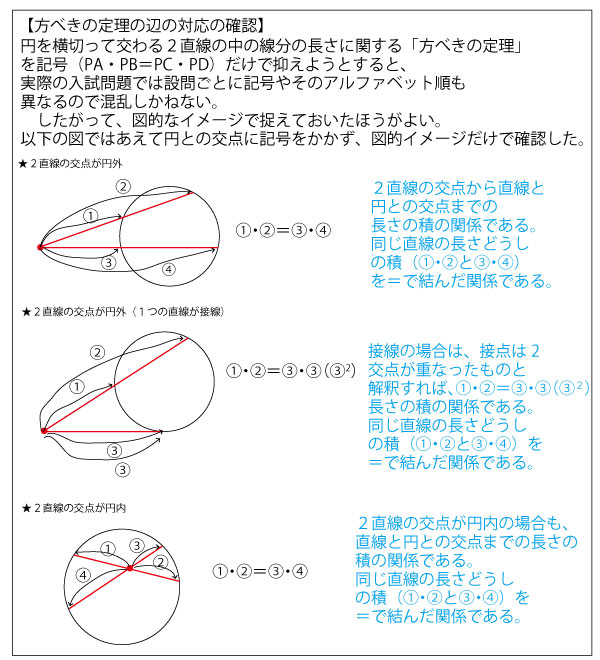
LM・LK=サシ(3点)
である。
これからLM・LKを求めるためには、何の定理を使うのか?また既に求めたIJの長さをどう活用するかを考える。