2023年千葉県公立高校入試「数学」第4問（総合問題）（配点18点）問題・解答・解説

2023年8月26日 2023年9月26日

asakura

2023年8月26日　船橋市議・予備校講師　朝倉幹晴

2023年2月に実施された千葉県公立高校入試「数学」第4問（総合問題）（18点）の解答・解説を作成しました。また千葉県教育委員会が発表した正答率・無答率も付記しました。学習や入試対策にご活用ください。

2023年第4問（18点）

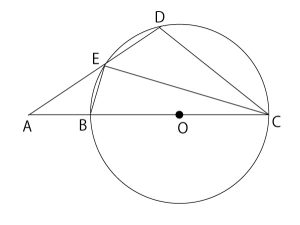
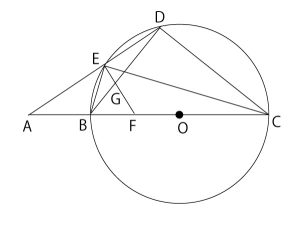
2人でじゃんけんをして、次のルールにしたがって点数を競う（きそう）ゲームがある。このゲームについて、下の会話文を読み、あとの（1）、（2）の問いに答えなさい。

ルール
・じゃんけんを1回するごとに、勝った人は出した手に応じて加点され、負けた人は出した手に応じて原点される。
・グーで勝つと1点、チョキで勝つと2点、パーで勝つと5点が加点される。
・グーで負けると1点、チョキで負けると2点、パーで負けると5点が減点される。
・あいこの場合は1回と数えない。
・最初の持ち点は、どちらも0点とする。

会話文
生徒Ｘ：例えば、ＡさんとＢさんが1回じゃんけんをして、Ａさんがチョキ、Ｂさんがパーを出したとき、それぞれの持ち点は、Ａさんが2点、Ｂさんが－５点になるということでしょうか。
教師Ｔ：そうですね。では、ＡさんとＢさんが3回じゃんけんをして、次のような手を出した結果、Ａさんの持ち点は何点になるでしょうか？

生徒Ｘ：（a）点です。
教師Ｔ：そのとおりです。それでは、2人がどのような手を出したのかがわからない場合を考えてみましょう。
ＡさんとＢさんが3回じゃんけんをして、Ａさんが2回勝ち、Ｂさんが1回勝った結果、Ａさんの持ち点　　　　　　　　が９点だったとき、Ｂさんの持ち点を求めてみましょう。
生徒Ｘ：まず、Ａさんが勝った2回の加点の合計を考えます。例えば、2回ともグーで勝った場合は加点の合計が2点となり、グーとチョキで勝った場合は加点の合計が3点となります。このように考えていくと、勝った2回の加点の合計は全部で（b）通り考えることができます。
このうち、Aさんが負けた1回の減点を考えた上で、3回じゃんけんをした結果、Aさんの持ち点が9点となりうる場合は1通りのみです。このことから、3回じゃんけんをした結果、Bさんの持ち点が（ｃ）点となることがわかります。
教師Ｔ：そうですね。じゃんけんの回数が少なければ、１つずつ考えることができますね。では、回数が多くなった場合について考えてみましょう。
次の表は、じゃんけんを1回だけしたときのＡさんとＢさんの手の出し方と、持ち点をまとめたものです。この表を見て気がつくことはありますか。

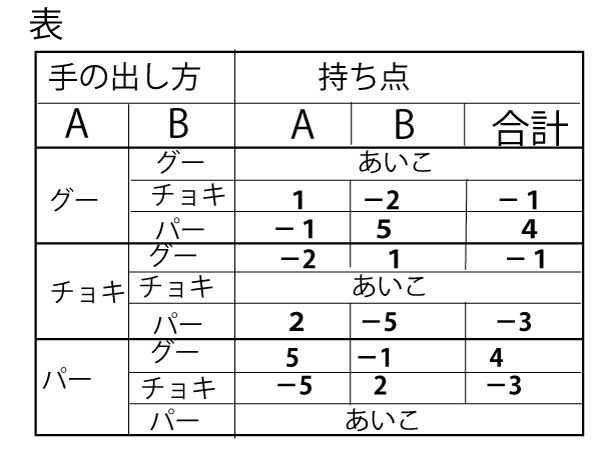
生徒Ｘ：2人の手の出し方は3通りずつありますが、あいこの場合は1回と数えないため、2人の手の出し方の組み合わせは、全部で６通り考えればよいというということになります。
また、じゃんけんを1回だけした結果、ＡさんとＢさんの持ち点の合計は、どちらかがグーで勝った場合は－1点、どちらかがチョキで勝った場合は－3点、どちらかがパーで勝った場合は4点となっています。
教師Ｔ：そうですね。2人の持ち点の合計で考えると、3通りになりますね。では、ＡさんとＢさんが10回じゃんけんをしたとき、どちらかがグーで勝った回数をa回、どちらかがチョキで勝った回数をb回、どちらかがパーで勝った回数をｃ回とすると、ｃはaとbを使ってどのように表すことができるでしょうか。また、10回じゃんけんをした結果の、2人の持ち点の合計をＭ点としたとき、Ｍをaとbを使って表すとどのようになりますか。
生徒Ｘ：ｃ＝（d）、M＝（e)と表すことができます。
教師T：そのとおりです。2人の持ち点の合計について、この式を用いると、aとbとcの組み合わせがどのようになるのかが考えやすくなりますね。