2023年共通テスト数学１A第1問［2］(2)（空間図形）（配点10点）問題・解答・解説

2023年9月17日　船橋市議・予備校講師　朝倉幹晴

2023年大学入試共通テスト第1問［2］（2）（立体図形）（配点10点）の解答・解説を作成しました。勉強や入試対策に役立ててください。問題の最後の２をクリックすると解答・解説のページに飛びます。

2023年共通テスト「数学１A」第1問［2］(2)（立体図形）（配点10点）

半径が5である球Sがある。この球面上に3点P、Q、Rをとったとき、これら3点を通る平面α上でPQ＝3、QR=5、RP=9であったとする。
球Sの球面上に点Tを三角錐（すい）TRQRの体積が最大となるようにとるとき、その体積を求めよう。
まず、
（2点）

であることから、△PQRの面積は
（3点）
である。
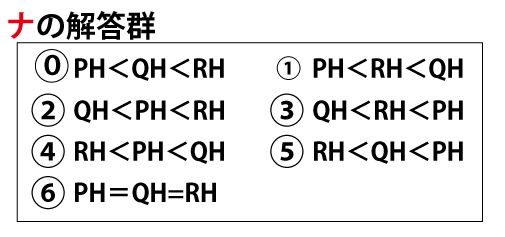
次に、点Tから平面αに垂直な直線を引き、平面αとの交点をHとする。このとき、PH、QH、RHの長さについて

ナ（2点）が成り立つ。

以上より、三角錐TPQRの体積は

（３点）である。