2023年大学入試共通テスト「数学IA」第5問(選択、20点)問題・解答・解説
2025年1月9日追記
2023年共通テスト、数学ⅠAの全問題解説動画作りました。
ご覧ください。
【動画80分】#共通テスト #数学ⅠA #2023年 解答解説
2023年12月14日 予備校講師・船橋市議 朝倉幹晴
2023年大学入試共通テスト「数学1A」第5問(選択、配点20点)の解答・解説を作成しましたので、ご活用ください。問題文の最後の所でページ番号「2」をクリックすると解答・解説に飛びます。
2023年大学入試共通テスト「数学IA」第5問(選択、20点)
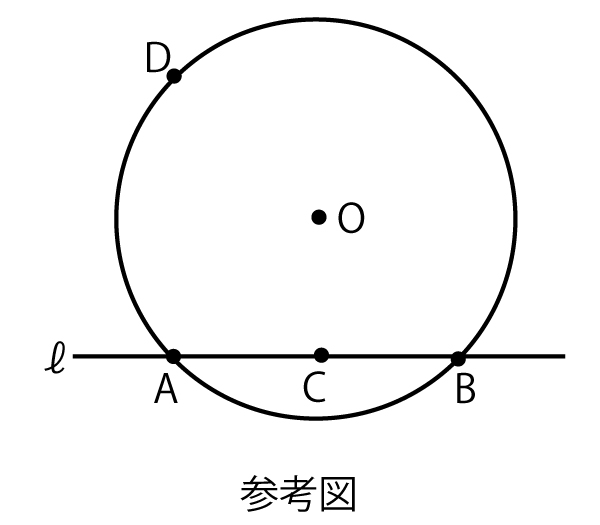
(1)円Oに対して、次の手順1で作図を行う。
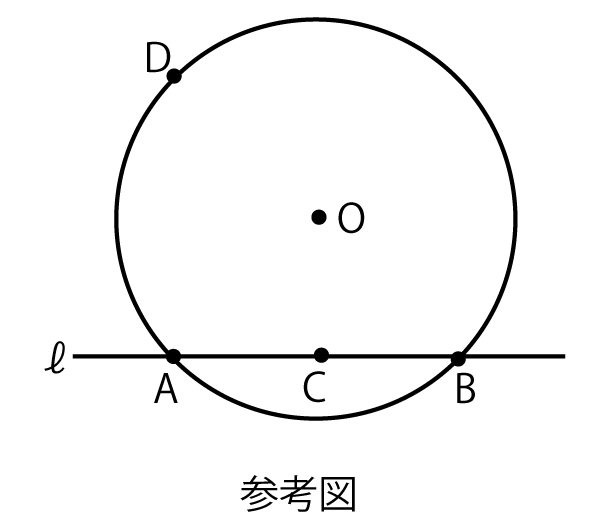
手順1
(Step1)円Oと異なる2点で交わり、中心Oを通らない直線ℓを引く。円Oと直線ℓとの交点をA、Bとし、線分ABの中点Cをとる。
(Step2)円Oの周上に、点Dを∠CODが鈍角となるようにとる。直線CDを引き、円Oとの交点でDとは異なる点をEとする。
(Step3)点Dを通り直線OCに垂直な直線を引き、直線OCとの交点をFとし、円Oとの交点でDとは異なる点をGとする。
(Step4)点Gにおける円Oの接線を引き、直線ℓとの交点をHとする。
このとき、直線ℓと点Dの位置によらず、直線EHは円Oの接線である。このことは、次の構想に基づいて、後のように証明できる。
構想
直線EHが円Oの接線であることを証明するためには、∠OEH=アイ°(2点)であることを示せばよい。
手順1の(Step1)と(Step4)により、4点C、G、H、ウ(2点)は同一円周上にあることがわかる。よって、∠CHG=エ(3点)である。一方、点Eは円Oの周上にあることから、エ=オ(3点)がわかる。よって、∠CHG=オであるので、4点C、G、H、カ(2点)は同一円周上にある。この円が点ウを通ることにより、∠OEH=アイ°を示すことができる。

(2)円Oに対して、(1)の手順1とは直線ℓの引き方を変え、次の手順2で作図を行う。
手順2
(Step1)円Oと共有点をもたない直線ℓを引く。中心Oから直線ℓに垂直な直線を引き、直線ℓとの交点をPとする。
(Step2)円Oの周上に、点Qを∠POQが鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。
(Step3)点Qを通り直線OPに垂直な直線を引き、円Oとの交点でQとは異なる点をSとする。
(Step4)点Sにおける円Oの接線を引き、直線ℓとの交点をTとする。
このとき、∠PTS=キ(3点)である。