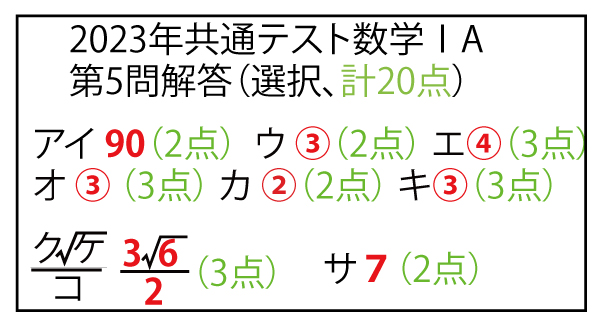
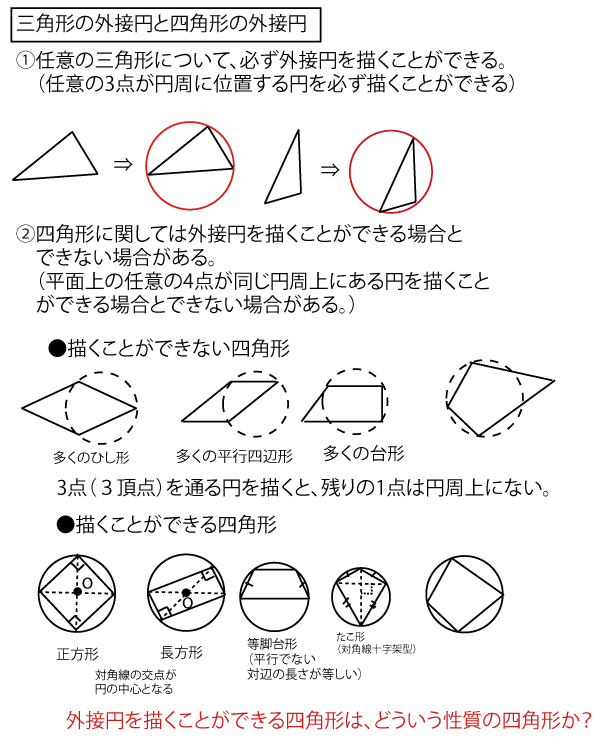
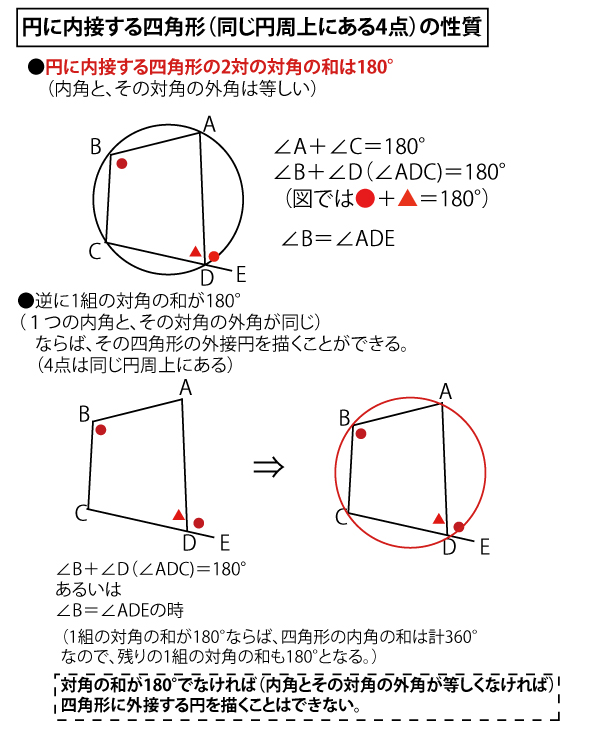
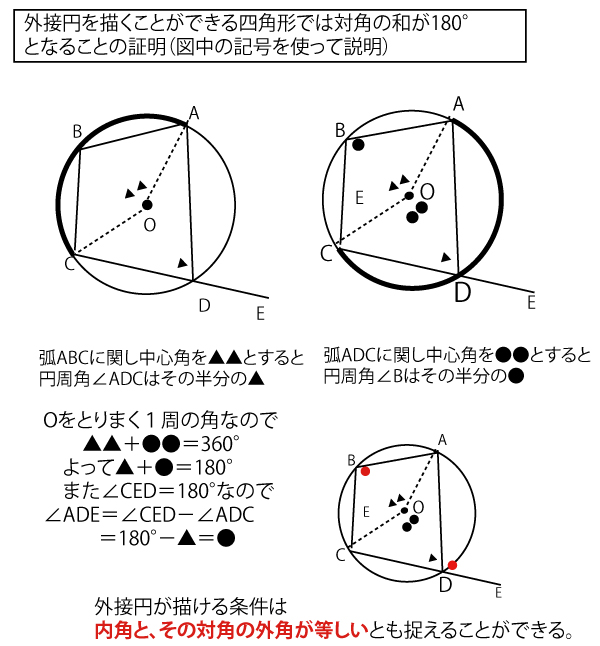
2023年大学入試共通テスト「数学IA」第５問（選択、20点）問題・解答・解説

【解説】
アイ

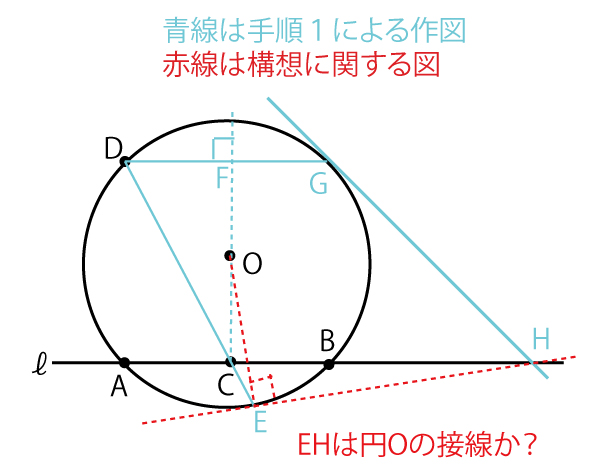
円の接線は接点と中心を結ぶ半径と直交するので、∠EOH＝90°（アイ答）（2点）であることが示されれば、EHが円の接線であることが証明できる。

ウ・エ

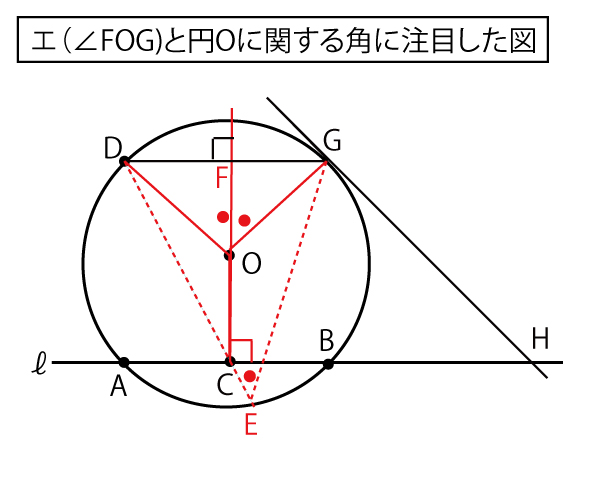
「（Step1)と(Step4)により、4点Ｃ、Ｇ、Ｈ、ウ（2点）は同一円周上にあることがわかる。」という設問で注目しているように、C・G・Hを円周に含む円に注目して図を描くと以下のようになる。

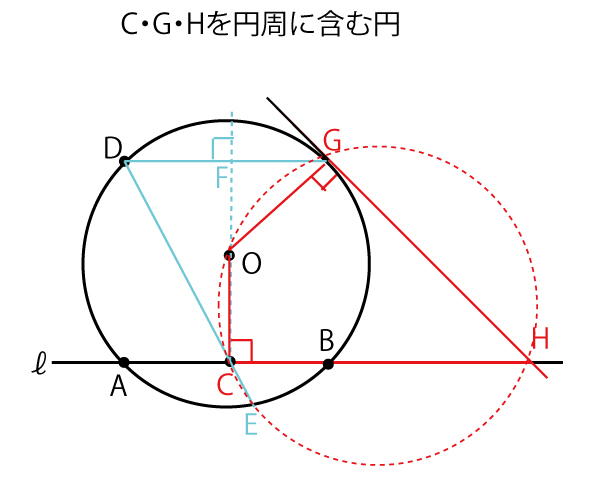
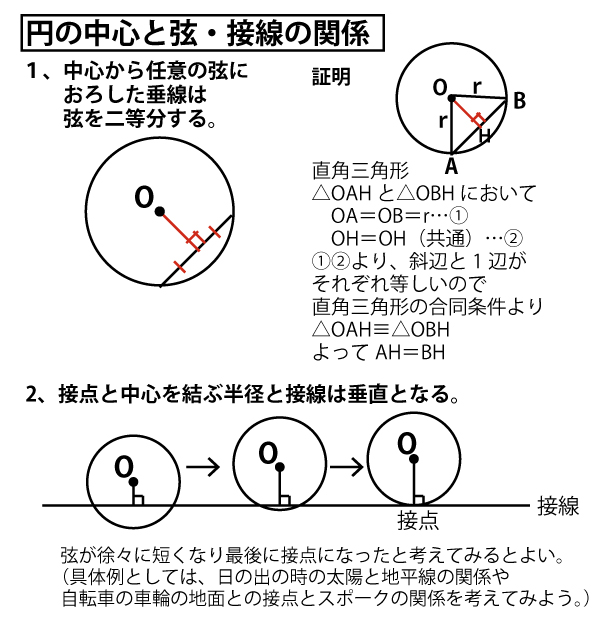
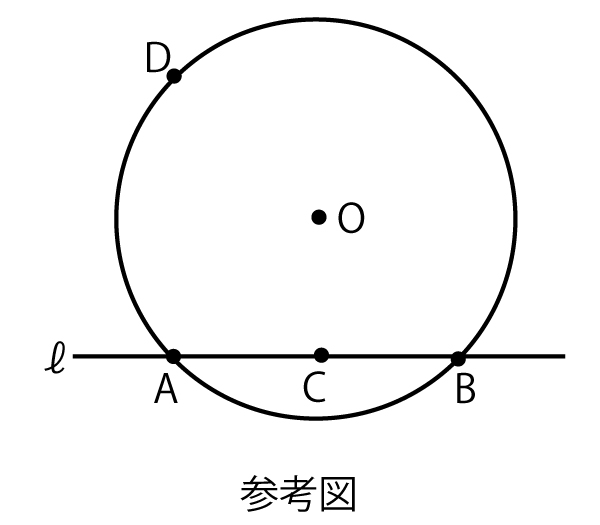
中心Oから弦に引いた垂線は、弦を垂直に二等分する。Cは弦ABの中点なのでなので、Oから弦ABに引いた垂線となり、∠OCB＝90°
また、中心と接点を結ぶ半径は接線と直交するので、∠ＯＧＨ＝90°。
四角形ＯＣＨＧで対角である∠OCB＋∠OGH＝90°＋90°＝180°。四角形の対角の和が180°のとき、四角形は円に内接する（四角形の4頂点を通る円を描ける）ので、Ｃ、Ｈ、Ｇ、Ｏ（ウ答）（）（2点）は同一円周上にあることがわかる。

円に内接する四角形では１つの内角とその対角の外角は等しいので、
∠ＣＨＧ＝∠ＦＯＧ（エ答）（）（3点）。

 

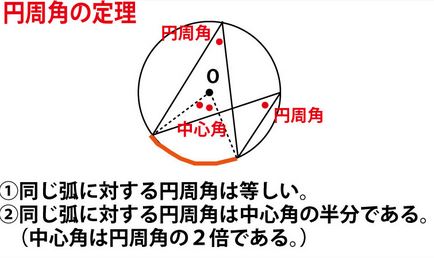
★円と弦・接線の関係、外接円と内接円の知識のまとめ

。

オ

OFは弦DGを垂直に二等分するので、エ（∠FOG）＝∠FOD（図の●）
よって弧DGに対する中心角∠DOG＝∠FOG＋∠FOD＝２∠FOG
円周角は中心角の半分なので、
円Oでの弧DGに対する円周角
∠DEG（オ答、）（3点）

＝１／２　×∠DOG＝１／２　×２∠FOG＝∠FOG（エ）

一方、点Ｅは円Ｏの周上にあることから、エ（∠FOG）＝オ（3点）がわかる。

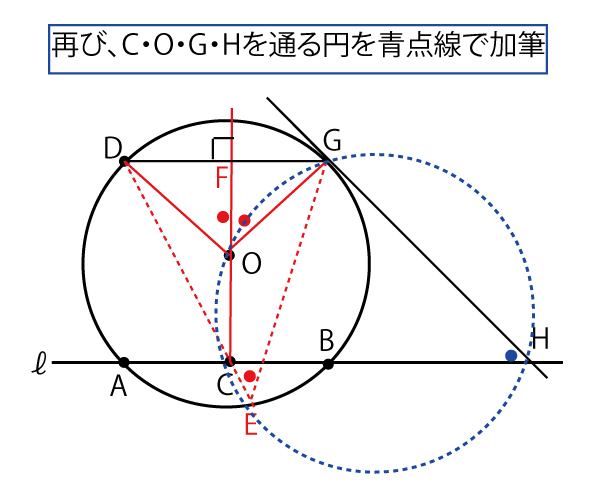
よって、青点線円の弧CGに対する円周角なので
∠ＣＨＧ（図の●）＝オ（∠DEG）であるので、
4点Ｃ、Ｇ、Ｈ、カ（E）（）（2点）は同一円周上にある。
つまり、この円が点ウ（O）を通ることにより、C、G、H、E、Oの5点は、全て青点線の円周上にある。
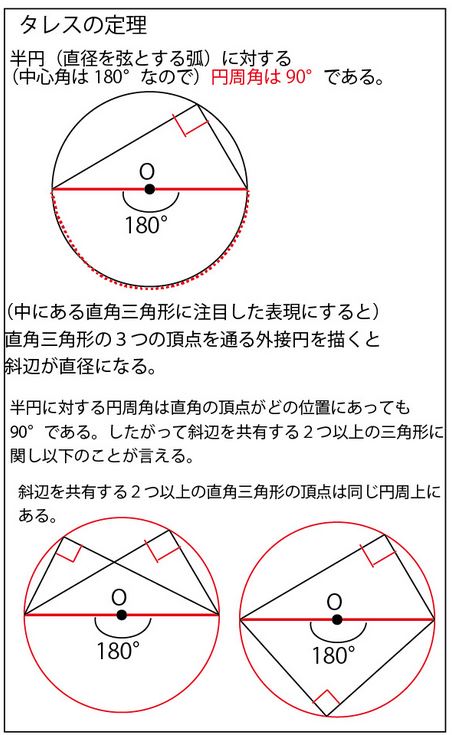
∠ＯＣＨ＝∠ＯＧＨ＝90°なので、タレスの定理より、ＯＨはこの円の直径である。よって∠ＯＥＨも直径を弦とする半円の弧に対する円周角なので、∠ＯＥＨ＝アイ（90）°を示すことができる。

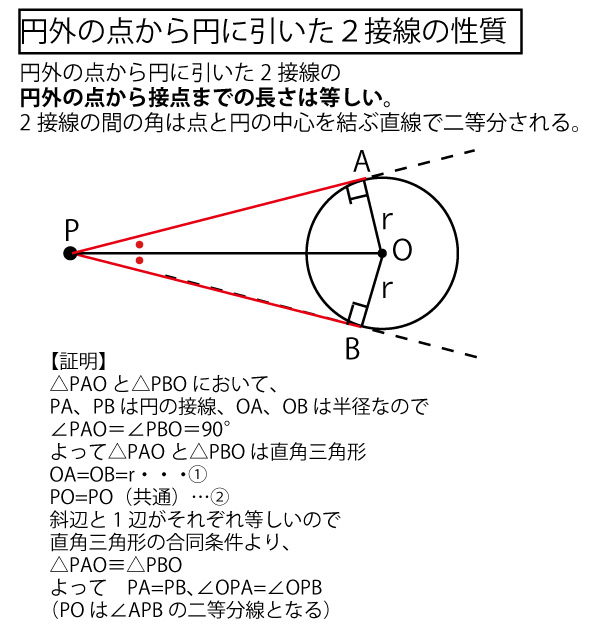
★円周角の定理とタレスの定理のまとめ

 

 

キ

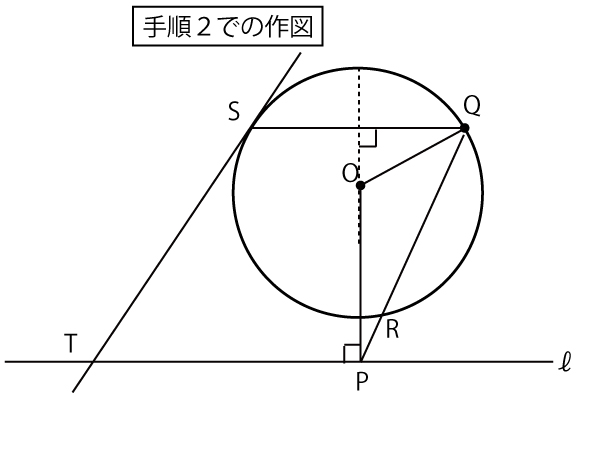
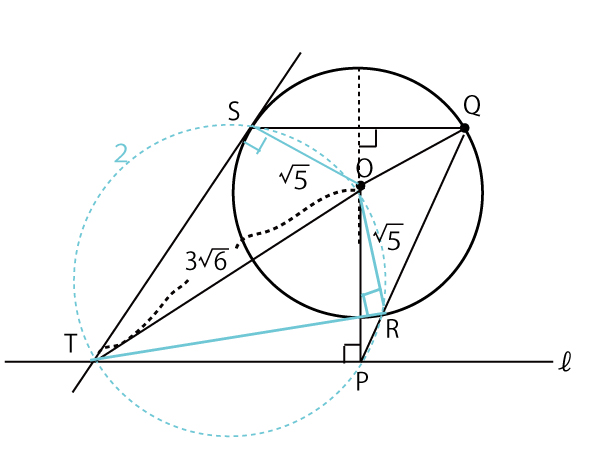
数学の入試問題全般もその傾向があるが、共通テスト「数学」の場合は、特に前問を解いた発想を使って、後半の問題を解かせることが多い。この図に前問で進めてきた思考パターンの流れに沿って思考と図への加筆をしていくと以下のようになるい。

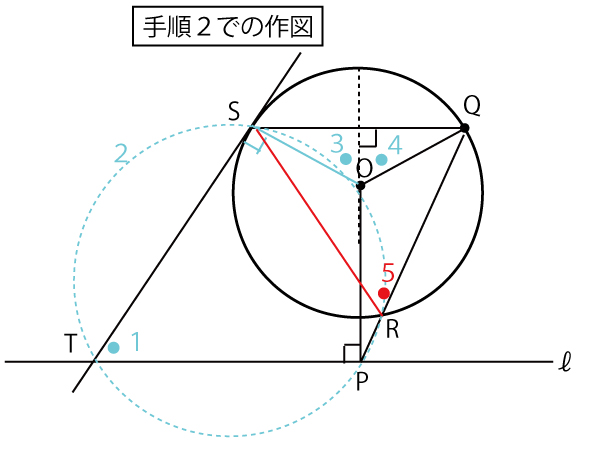
１（設問が聞いている∠PTS●）→２（S・T・P・Oを円周に含む円を考える）
→３（円に内接する四角形である内角のその対角の外角は等しい●）→３と４は等しく中心角∠SOQは●●となる→５（円Oで弧SQに対する円周角（∠QRS）は中心角の半分で●となる）。よって∠PTS＝∠QRS（キ答）（）（3点）

これも前問の発想と同じ流れで、四角形PTSRにおいて内角∠PTSとその対角の外角∠QRSは等しいので、P・T・S・Rは同じ円周上にあり、あわせてP・T・S・R・Oは同じ図の青点線の円周上にある。

ＳＴは円Ｏでの接線なので∠ＯＳＴ＝90°。この青点線の円（Ｏ・Ｐ・Ｒを通る円）でタレスの定理より、ＯＴは直径となる。