2024年　＃大学入試　＃共通テスト　＃数学１A　第1問［2］（配点20点）問題・解答・解説

2024年4月18日 2024年4月24日

asakura

2024年4月17日　　予備校講師・船橋市議　朝倉幹晴

2024年大学入試共通テスト第1問［2］（配点10点）の解答・解説を作成しました。勉強や入試対策に役立ててください。問題の最後の２をクリックすると解答・解説のページに飛びます。
入試問題は黒一色印刷ですが、せっかくの画面上なので一部カラー化しています。

大学入試共通テスト数学１A第1問［２］（配点20点）問題

以下の問題を解答するにあたっては、必要に応じて末尾の三角比の表を用いてもよい。
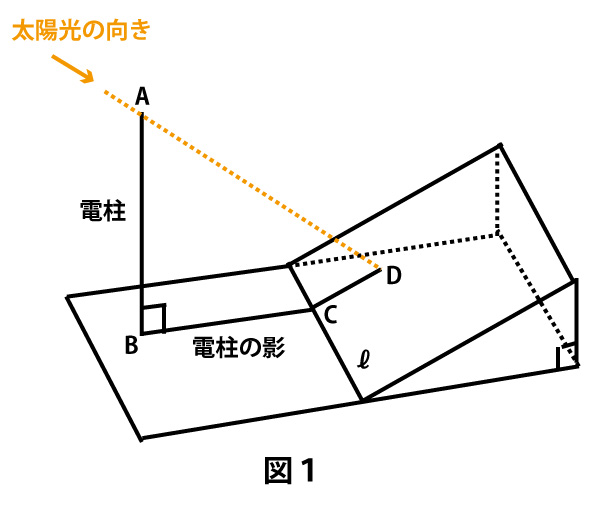
水平な地面（以下、地面）に垂直に立っている電柱の高さを、その影の長さと太陽高度を利用して求めよう。
図１のように、電柱の影の先端は坂の斜面（以下、坂）にあるとする。また、坂には傾斜を表す道路標識が設置されていて、そこには７％と表示されているとする。
電柱の太さと影は無視して考えるものとする。かた、地面と坂は平面であるとし、地面と坂が交わってできる直線はℓとすり。
電柱の先端を点Aとし、根もとを点Bとする。電柱の影について、地面にある部分を線分BCとし、坂にある部分を線分CDとする。線分BC、CDがそれぞれℓと垂直であるとき、電柱の影は坂に向かってまっすぐにのびているということにする。

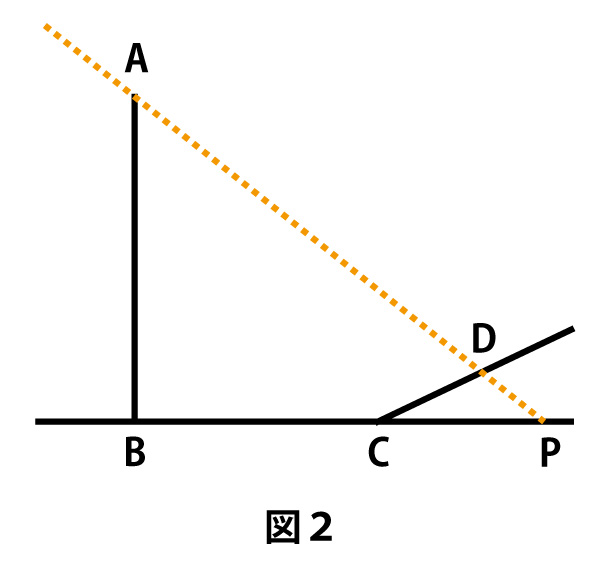
電柱の影が坂に向かってまっすぐにのびているとする。このとき、４点A、B、C、Dを通る平面はℓと垂直である。その平面において、図２のように、直線ADと直線BCの交点をPとすると、太陽高度とは∠APBの大きさのことである。

道路標識の7%という表示は、この坂をのぼったとき、100ｍの水平距離に対して7mの割合で高くなることを示している。nを１以上９以下の整数とするとき、坂の傾斜角∠DCPの大きさについて
n°＜∠DCP＜n°＋1°
を満たすnの値はシである。
以下では、∠DCPの大きさは、ちょうどシ°であるとする。

ある日、電柱の影が坂に向かってまっすぐにのべていたとき、影の長さを調べたところBC=7m、CD=4mであり、太陽高度は∠APB＝45°であった。点Ｄから直線ABに垂直な直線を引き、直線ABとの交点をEとするとき
BE＝ス×セｍ
であり
DE＝（ソ＋タ×チ）m
である。よって、電柱の高さは、小数第２位で四捨五入するとツｍであることがわかる。