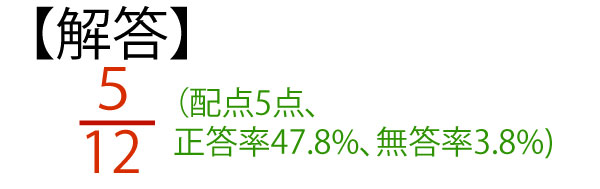
2018年前期千葉県公立高校入試「数学」第2問（4）（確率）（配点5点）問題・解答・解説

【解説】

素数とは、１とそれ自身以外に約数を持たない2以上の自然数のこと（１は含まない）。素数では２のみが偶数で、残りはすべて奇数である（4以上の偶数は２×●のように、２と●を約数として持つ）。
さいころの目の数の和は２～12である。それぞれ素数かどうか考えてみよう。

２（素数）
３（素数）
４＝２×２（２²）（素数ではない）
５（素数）
６＝２×３（素数ではない）
７（素数）
８＝2³（素数ではない）
9=３²（素数ではない）
10＝２×５（素数ではない）
11（素数）
12＝２²×３（素数ではない）

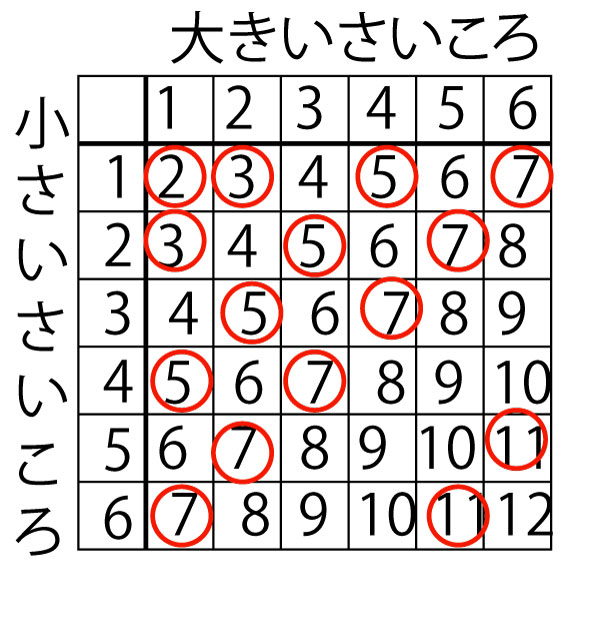
碁盤目表で和が２・３・５・７・11となる目を数える。

碁盤目表を全部うめなくても、下図のように青線に対して線対称であることを利用すればより簡単に考えられる。

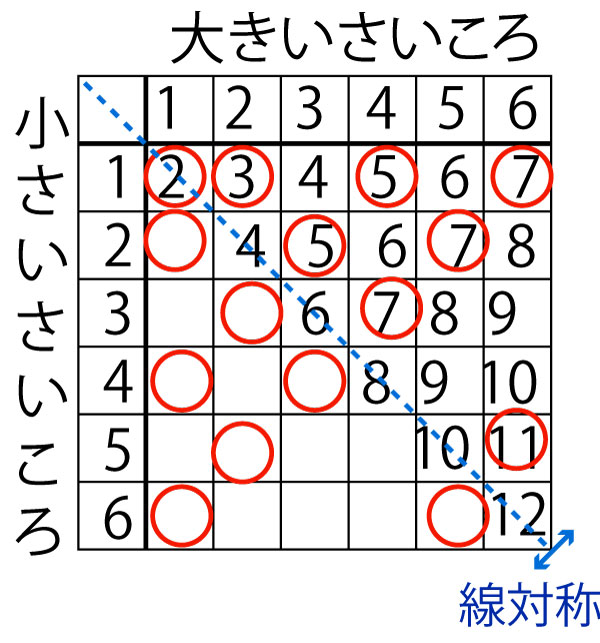
36マス分の15ますなので15／36で５／12。