2020年大学入試センター試験「数学ⅠA」第1問［２］（配点８点）、問題・解答・解説

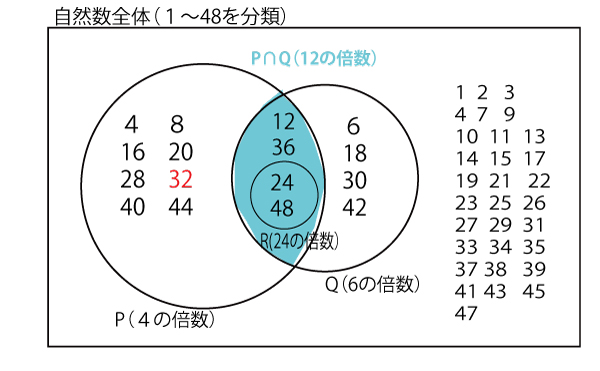
これらの集合の関係をベン図に描くと以下のようになる。なお下図で具体的に書き込んだ数は１～48までにしたが、実際は同じような繰り返しで数は無限に続く。

数を列に並べて記すと以下のようになる。

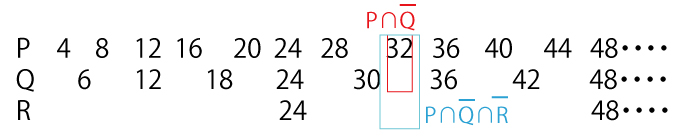
32∈スの答となりうるように、P、Q、Rで示した集合は、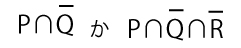

であるが後者の選択肢はないため、答は前者となる。

（２）P∩Qは12の倍数であり、その中で最小のものは12（セソの答）、ただこれは24の倍数（R）の中に含まれない（）。

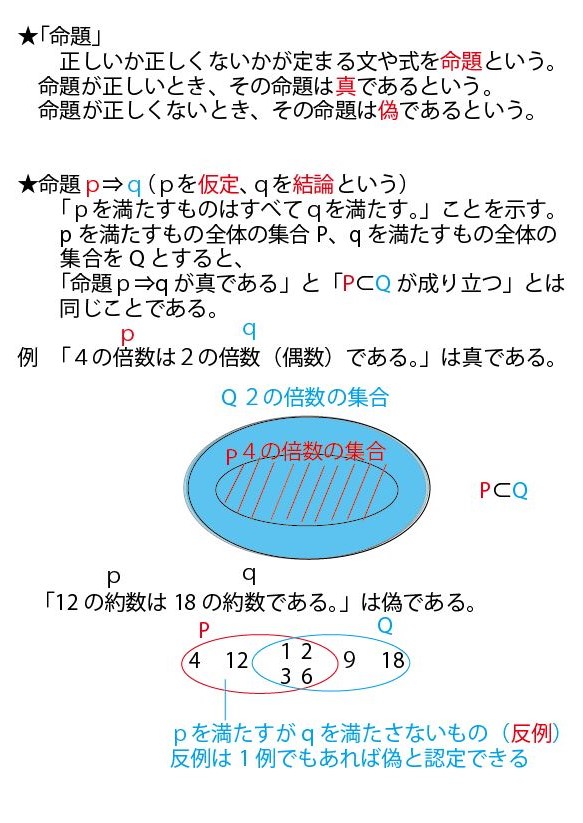
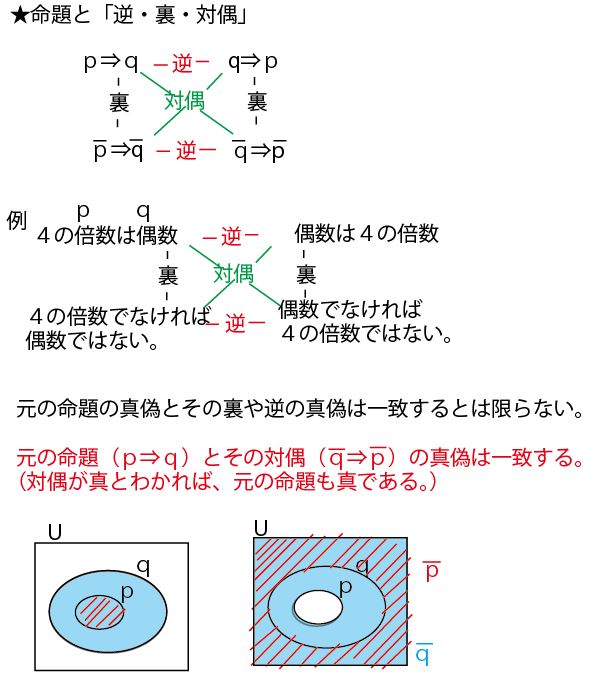
（3）命題「A⇒B」が偽であることを示したい時は、「AであるのにBではない」という例が1例でもあればよい。このような例を、命題「A⇒B」に対する反例という。
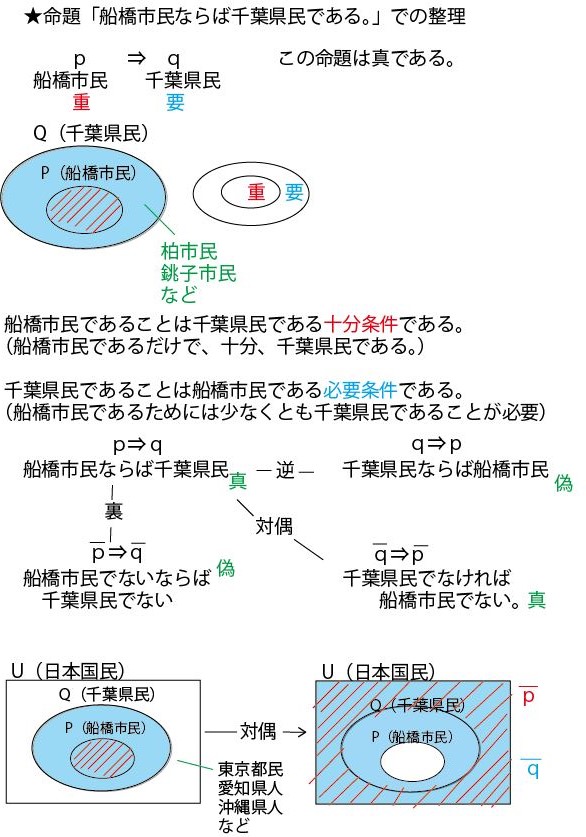
たとえば、命題「４の倍数⇒２の倍数」は真なので反例はない。命題「２の倍数⇒４の倍数」は偽であり、「２の倍数であるのに４の倍数ではない」２や６が反例となる。（別の例を出す。命題「船橋市民⇒千葉県民」は真なので反例はない。命題「千葉県民⇒船橋市民」は偽であり、市川市民や流山市民が反例となる。）

であり、命題「A⇒B」で12が「Aであるのに、Bでない」という例（反例）となっているのは、である。

ちなみに４つの命題を日本語で表現し、また、その真偽と、偽の場合の反例を示すと以下のようになる。

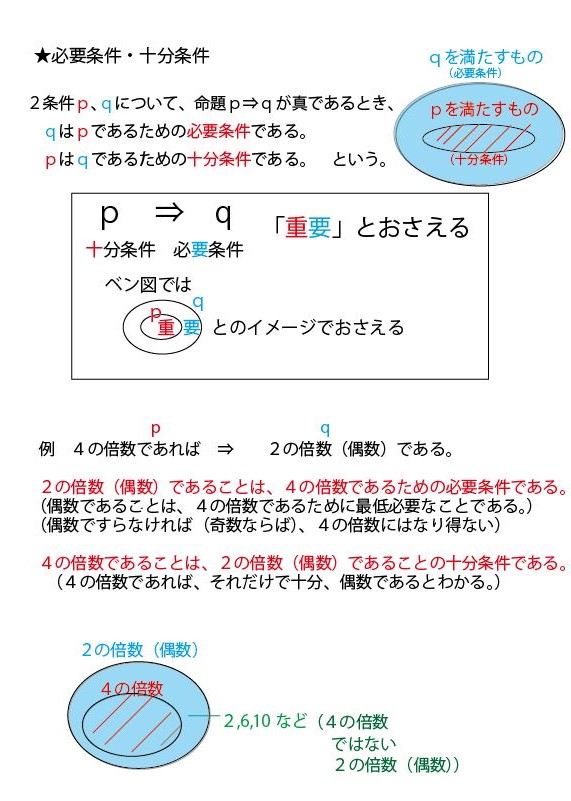
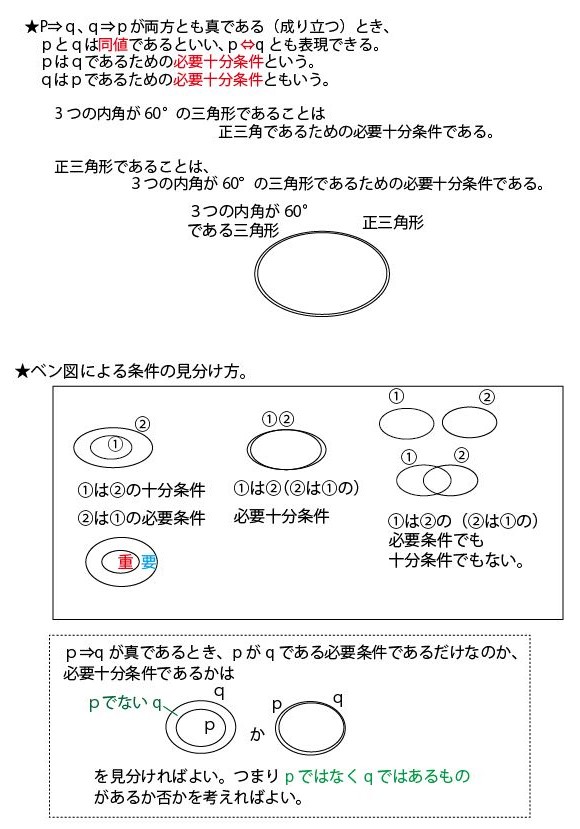
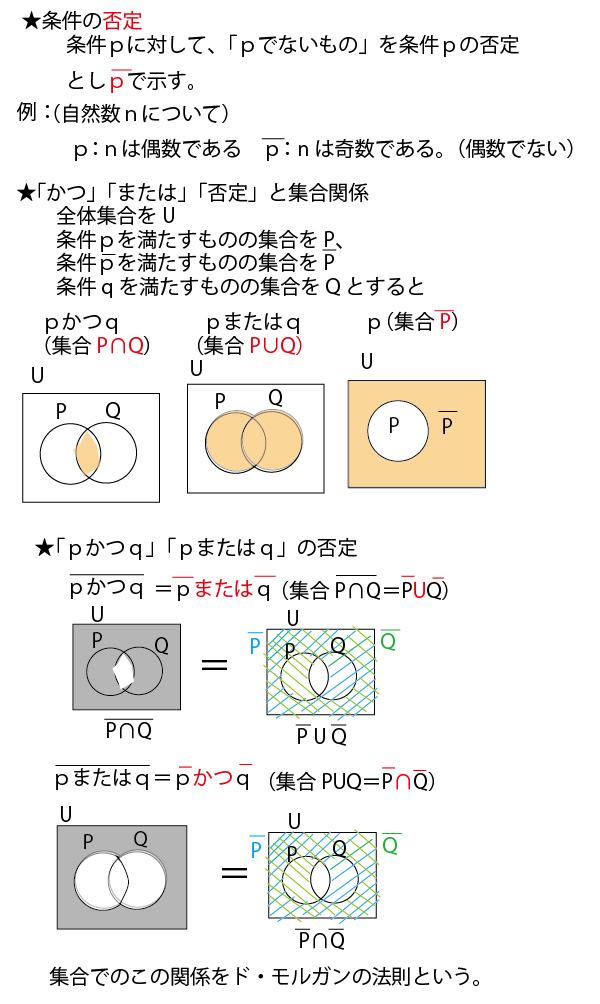
●集合と命題の基礎知識の整理

以上の解説で理解できる方はそれで大丈夫です。ただ、理解が不十分な方は、以下で「命題と集合」に関する考え方、特にベン図での捉え方を整理しますので、お読みください。前半は「4の倍数は２の倍数」を例に数学的に説明します。ただそれだけでは、イメージや理解が不十分の方のために最後に日本語的なたとえ「船橋市民は千葉県民である」で補足説明していますので合わせてご覧ください。