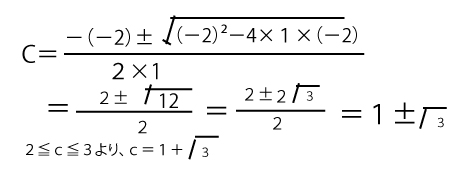2020年大学入試センター「数学ⅠA」第1問［３］（配点12点）、問題・解答・解説

解説

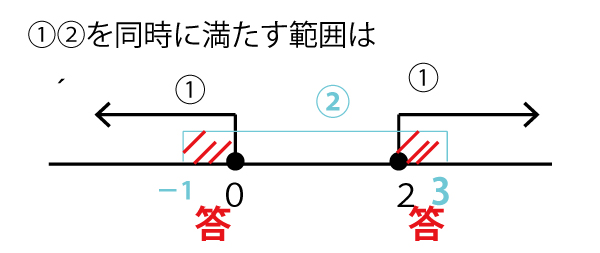
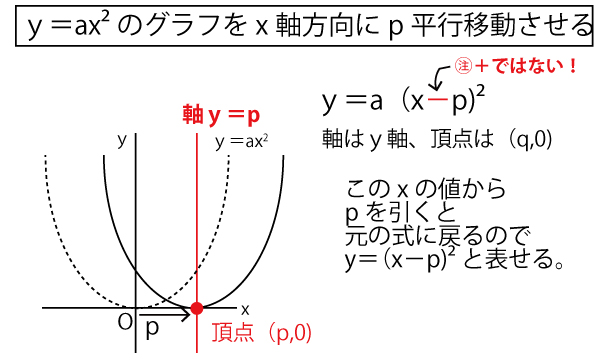
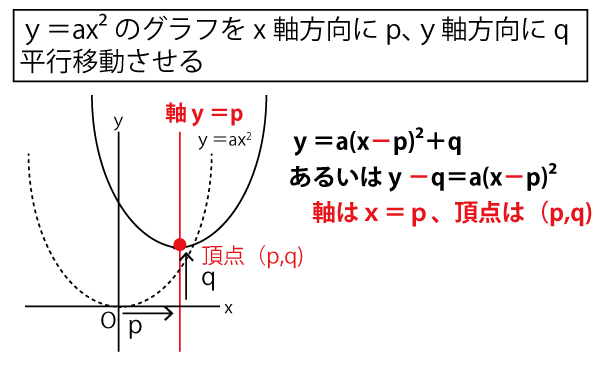
（1）平行移動した2次関数は、（c,0)(c+4,0)という、ｘ軸（ｙ＝0）上の2点を通る。ｃ、ｃ＋４を２つの実数解として持つ2次方程式でｘ^２の係数が１となるのは、（ｘーｃ）（ｘ－(ｃ＋４））＝０なので、この2次関数はｙ＝（x－ｃ）（ｘー（ｃ＋４））である。

展開して計算して、ｙ＝ｘ^２−（ｃ＋4）ｘーcx＋ｃ（ｃ＋4）
ｙ＝ｘ^２ー（2c+4）x＋ｃ（ｃ＋4）
y=x²−2(c+2)x+c(c+4)（ツテの答、2点）

参考、上記の発想を忘れてしまった場合の求め方（計算がたいへんなので上記の発想を使ったほうが簡略）

平行移動のため、傾き（ｘ²の係数）は変化しない。原点（0,0)を通っていた点が、ｙ＝x²＋ax+bとすると、これが（c、０）（c+4、０）を通るので、 ０＝c²＋ac+b・・・
０＝（c+4)²＋a(c+4)＋b＝c²＋8c＋16＋ac＋4a＋ｂ・・・ c²＋ac+b＝c²＋8c＋16＋ac＋4a＋ｂ 0=8c＋16＋4a ー4a＝8c+16 。a＝－2c－4＝－2(c+2)。
に代入して、 c²−2(c+2)c＋b＝０ ＝－c2＋2c2＋4c＝c²＋4c＝ｃ（ｃ＋4）

線分はｘ＝３（－３≦ｙ≦０）なので、共有点を持つためには、Ｇでｘ＝３のとき－３≦ｙ≦０となればよい。
Ｇにｘ＝３を代入すると、
ｙ＝3²−2(c+2)×３＋ｃ（ｃ＋4）＝９ー６（c+2)＋c²＋4c＝９－6c－12＋c²＋4c=c²−2c－３
－３≦c²ー2c－3≦０なので、－３≦ｃ²ー2c－３とc²ー2c－3≦０

を同時に満たすｃの範囲を求めればよい。

－３≦ｃ²ー2c－３
０≦c²ー2c
0≦c(c-2)
よってｃ≦０またはｃ≥２…
c²ー2c－3≦０
（c－3)（c+1)≦０
－1≦ｃ≦３…

－１≦ｃ≦０（トナの答、2点）、２≦c≦３（ニヌの答、2点）

（2）２≦ｃ≦３で、Ｇが（３、－1）を通るのでｘ＝３、ｙ＝－１を代入して
－１＝３²−2(c+2)・3+c(c+4)
－１＝９－6cー12＋c²＋4c
左辺・右辺を逆にして
９－6cー12＋c²＋4c＝－１
c²−2c－２＝０

Gを平方完成させると

y=x²−2(c+2)x+c(c+4)
＝x²−2(c+2)x＋（c+2)²−（c＋2）²＋ｃ（ｃ＋4）
＝（ｘ－（ｃ＋2））²−c²ー4c－4＋c²＋4c
=（ｘ－（ｃ＋2））²⁻4
ここにｃを代入すると

●二次関数とグラフのまとめ

様々な二次関数ｙ＝ax²＋bx²＋ｃのグラフは、ｙ＝ax²をｘ軸、ｙ軸方向に平行移動させたと捉えることができる。そう捉えると軸と頂点が決まり、図が描きやすく、座標の中での他の曲線・直線との位置関係がわかりやすくなる。ｙ＝ax²＋bx＋cをｙ＝a（x－p）²＋qのように変形することを平方完成といい、以下のような手順で変形をする。