2020年大学入試センター試験「数学IA」第2問[2](15点)問題・解答・解説
解説
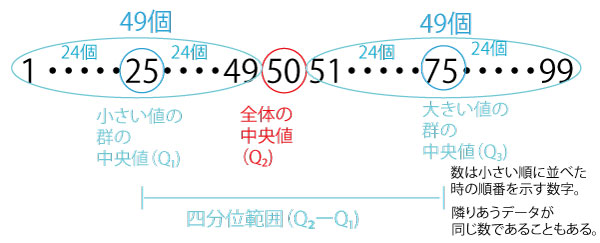
99個の観測値データを値の小さい順に並べ、小さい順に1~99の番号をつけて考えると以下のようになる。なお隣り合う数値は
左の値≦右の値であって、左の値<右の値とは限らない、つまり左の値=右の値がありうる点を注意してほしい。
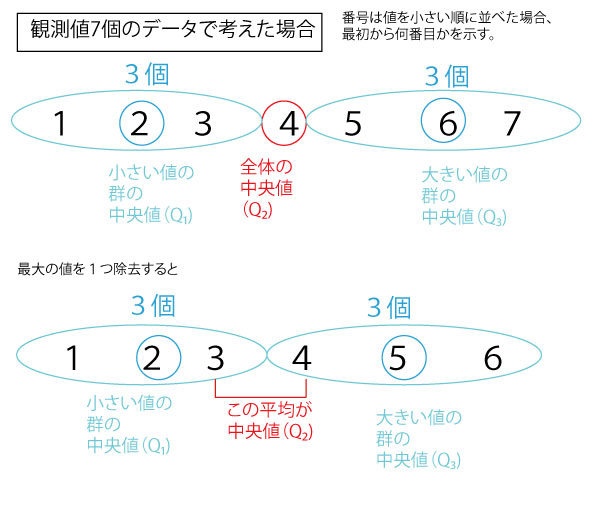
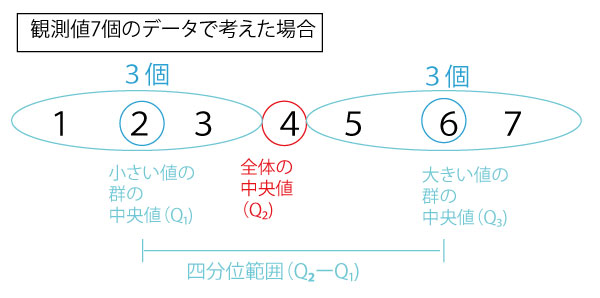
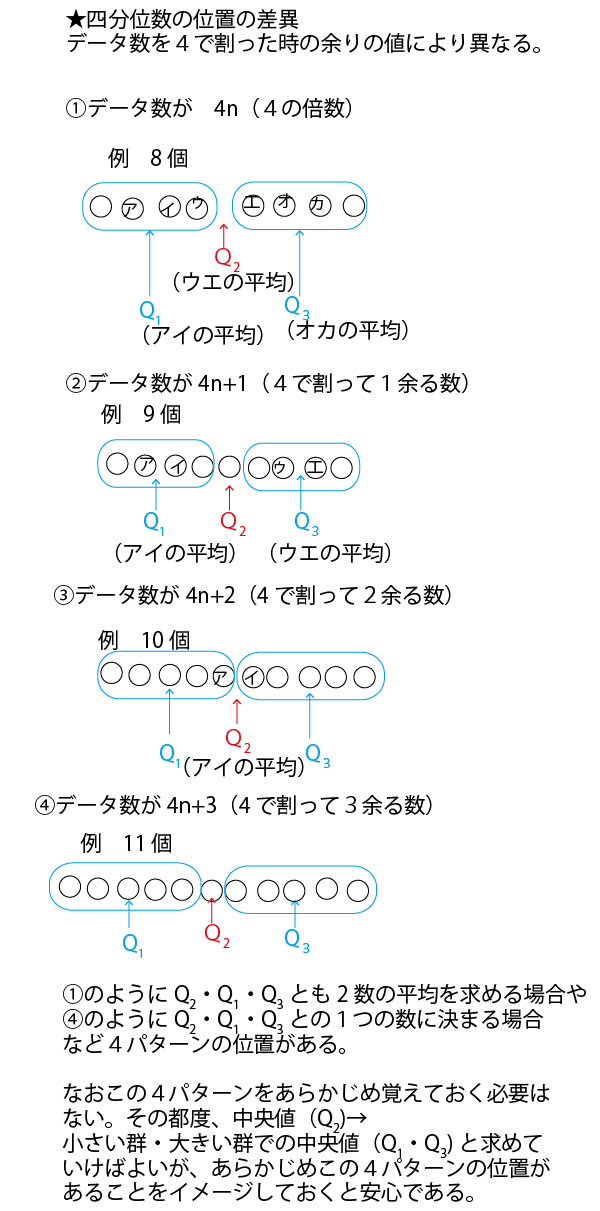
統計は多くの数のデータを把握・処理する上で有効だが、最初に学ぶ時、数が多いゆえにイメージがしにくくなることがある。最初の理解のためには少ない数のデータで考えることをお勧めする。本解説の末尾につけたまとめのようにQ1、Q2、Q3で区分される群は観測値の個数が4n、4n+1、4n+2、4n+3(nは0以上の整数)かによってパターン化される。99=4×24+3と同じパターンになる小さな個数7=4×1+3で考えてみよう。
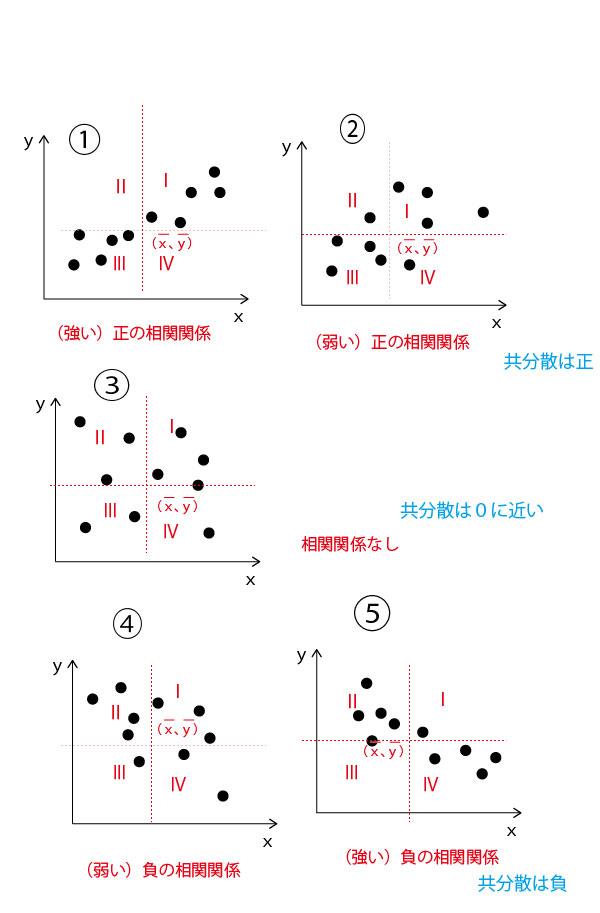
 平均値は第1四分位数と第3四分位数の間にある。×
平均値は第1四分位数と第3四分位数の間にある。×
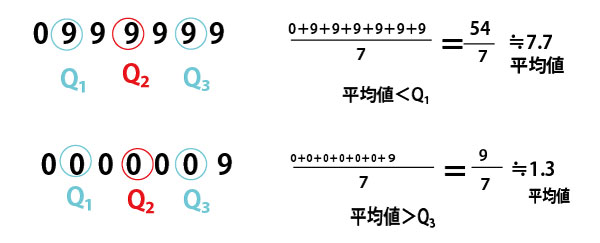
Q1(第1四分位数)より小さい値の群に極端に小さい値が多かった場合、逆にQ3(第3四分位数)より大きい値の群に極端に大きい値が多かった場合、平均値は極端に小さい値、大きい値に引きずられて、Q1より小さい、Q3より大きいとなる場合がある。
したがって×。7個のデータで考えると以下の例がそれにあたる。
 四分位範囲は標準偏差より大きい。×
四分位範囲は標準偏差より大きい。×
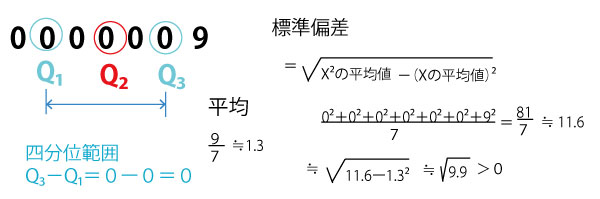
Q1=Q3=0であり、Q3以上に0より大きい数があった場合、四分位範囲はQ3-Q1=0で、標準偏差は0より大きくなるので、四分位範囲は標準偏差より小さくなる。よって×。以下が7個のデータでのその例である。
 中央値より小さい観測値の個数は49個である。×
中央値より小さい観測値の個数は49個である。×
![]()
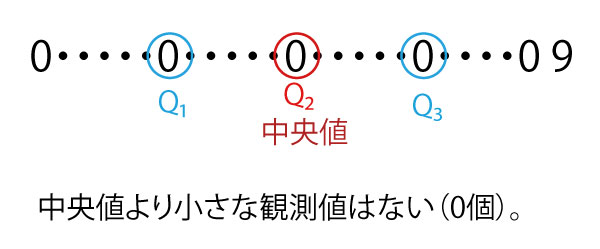
![]() は、データ一般の考え方なので7個データのモデルで考えられたが、今度は個数を特定しているので99個の測定値で考えてみよう。小さい値から98番目までがすべて0で、99番目が9だった測定値を考えると、中央値は0で、中央値より小さい数値はないので0個となる。隣り合うデータが同じ数であることがありうることを知っていれば49個とは限らないことがわかる。
は、データ一般の考え方なので7個データのモデルで考えられたが、今度は個数を特定しているので99個の測定値で考えてみよう。小さい値から98番目までがすべて0で、99番目が9だった測定値を考えると、中央値は0で、中央値より小さい数値はないので0個となる。隣り合うデータが同じ数であることがありうることを知っていれば49個とは限らないことがわかる。
 最大値に等しい観測値を1個削除しても第1四分位数は変わらない。〇
最大値に等しい観測値を1個削除しても第1四分位数は変わらない。〇
99個や7個のような4n+3で示される個数の場合、以下のようになる。7個の例で説明しよう。
第1四分位数が変わらないことがわかる。
 第1四分位数より小さい観測値と、第3四分位数より大きい観測値とをすべて削除すると、残りの観測値の個数は51個である。×
第1四分位数より小さい観測値と、第3四分位数より大きい観測値とをすべて削除すると、残りの観測値の個数は51個である。×
選択肢![]() の場合と同様、という隣り合うデータが同じ数であることがありうることを知っていれば、「Q1より小さい観測値」も「Q1より小さい観測値」も24個とは限らない。よってそれらを削除する数が48個とは限らないので、残りの観測地の個数は51個とは限らない。
の場合と同様、という隣り合うデータが同じ数であることがありうることを知っていれば、「Q1より小さい観測値」も「Q1より小さい観測値」も24個とは限らない。よってそれらを削除する数が48個とは限らないので、残りの観測地の個数は51個とは限らない。
 第1四分位数より小さい観測値と、第3四分位数より大きい観測値とをすべて削除すると、残りの観測値からなるデータの範囲はもとのデータの四分位範囲に等しい。〇
第1四分位数より小さい観測値と、第3四分位数より大きい観測値とをすべて削除すると、残りの観測値からなるデータの範囲はもとのデータの四分位範囲に等しい。〇
もとのデータの四分位範囲はQ3ーQ1となる。Q1より小さい観測値とQ3より大きい観測値全て削除すると、観測値の中で最小値は(もとの99個のデータでの)Q1、最大値はQ3となり、データの範囲はQ3-Q1となる。
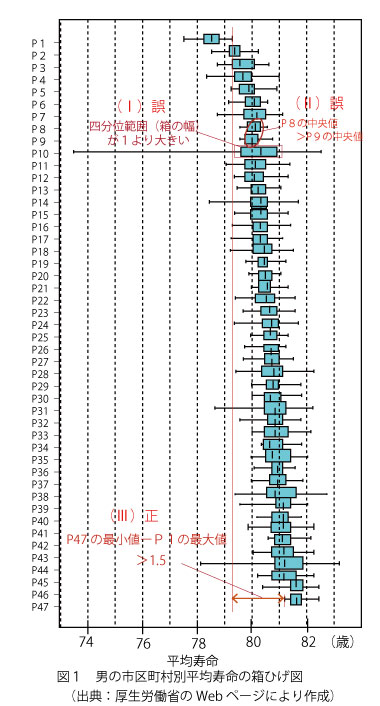
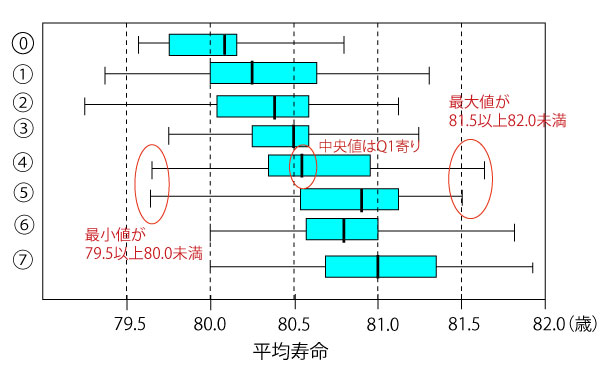
(2)図1は、平成27年の男の市区町村別平均寿命のデータを47の都道府県P1、P2、・・・・、P47ごとに箱ひげ図にして並べたものである。次の 、
、 、
、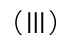 は図1に関する記述である。
は図1に関する記述である。
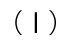 四分位範囲はどの都道府県においても1以下である。誤
四分位範囲はどの都道府県においても1以下である。誤
![]() 箱ひげ図は中央値が小さい値から大きい値に上から下へ並んでいる。誤
箱ひげ図は中央値が小さい値から大きい値に上から下へ並んでいる。誤
![]() P1のデータのどの値とp47のデータのどの値とを比較しても1.5以上の差がある。正
P1のデータのどの値とp47のデータのどの値とを比較しても1.5以上の差がある。正
(3)
最小値・最大値から![]()
![]() と推定できる。そして、中央値の位置からス
と推定できる。そして、中央値の位置からス![]() (3点)。
(3点)。
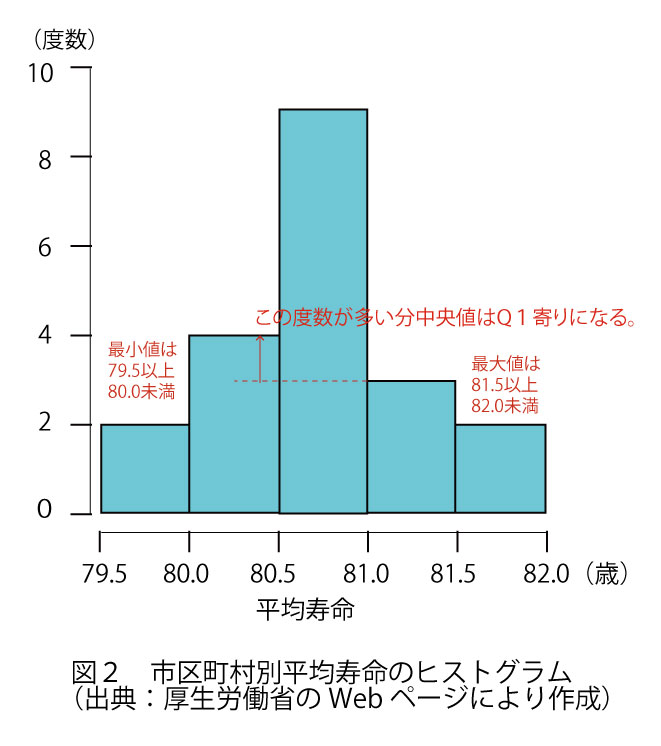
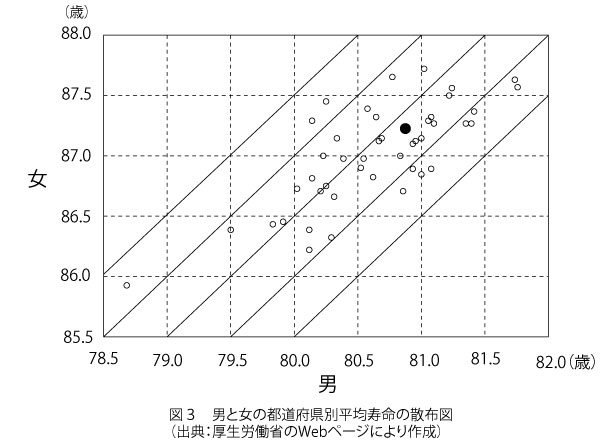
(4)ヒストグラムの階級の幅が0.25に設定されている。図3の年齢差を示す傾き1の曲線は0.5の幅なので、中央に線を入れて0.25ごとの幅にし、その中にある個数を数えると以下のようになる。ただし、線の引き方・見方によって、数が1・2程度ずれる(隣りの階級に含まれると解釈する)こともあるが、概数を読むことができれば選択肢を選ぶことができる。
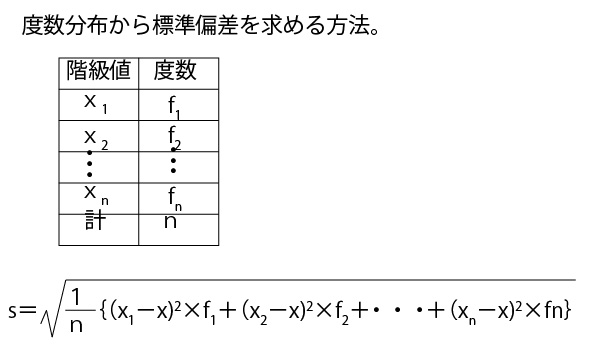
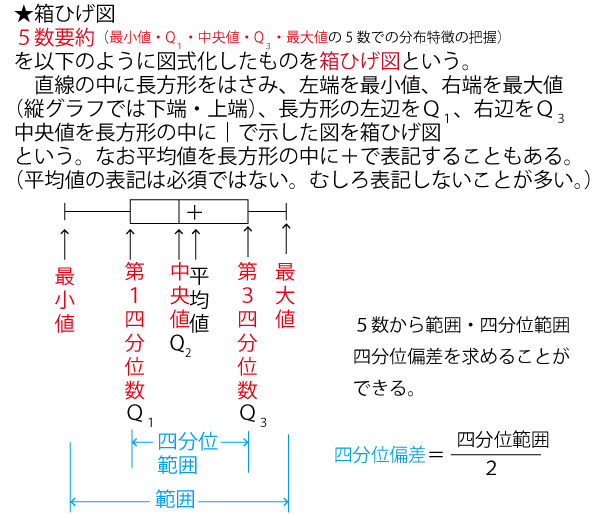
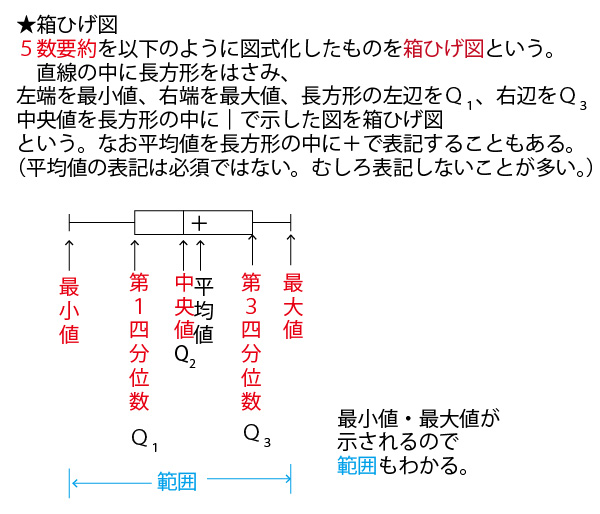
★【中学(中1「資料の整理」)】分野のまとめ


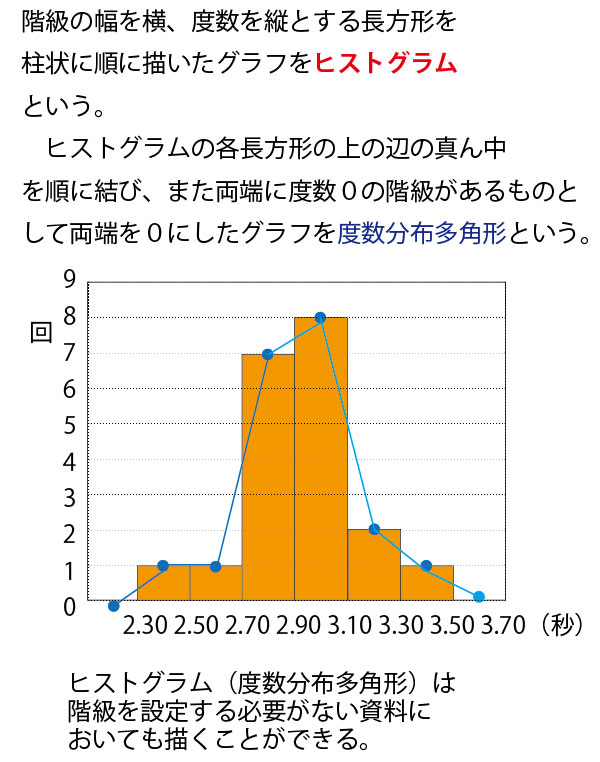
★高校数Ⅰ(データの分析)分野のまとめ。
中学1年で学ぶ「資料の整理」の発展編であり、この学問分野を統計学という。
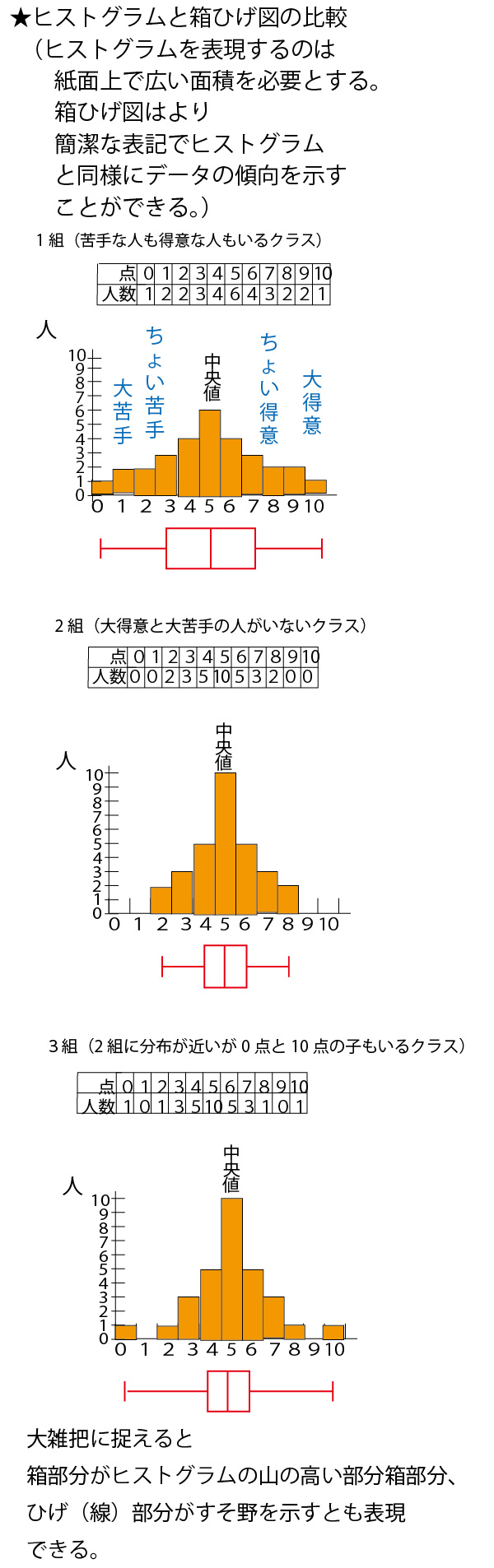
具体例として、数学の小テスト(10点満点)の平均点がいずれも5点が分布が異なる30人の7クラス(1組~7組)を例に考えていこう。
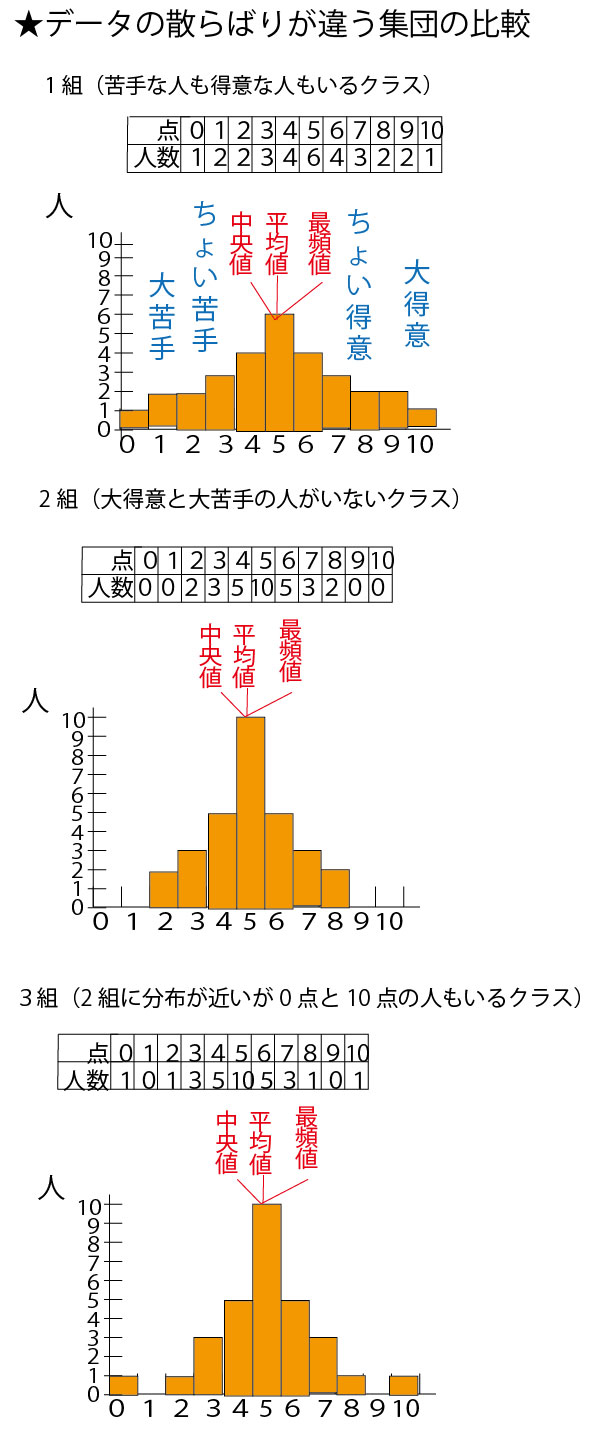
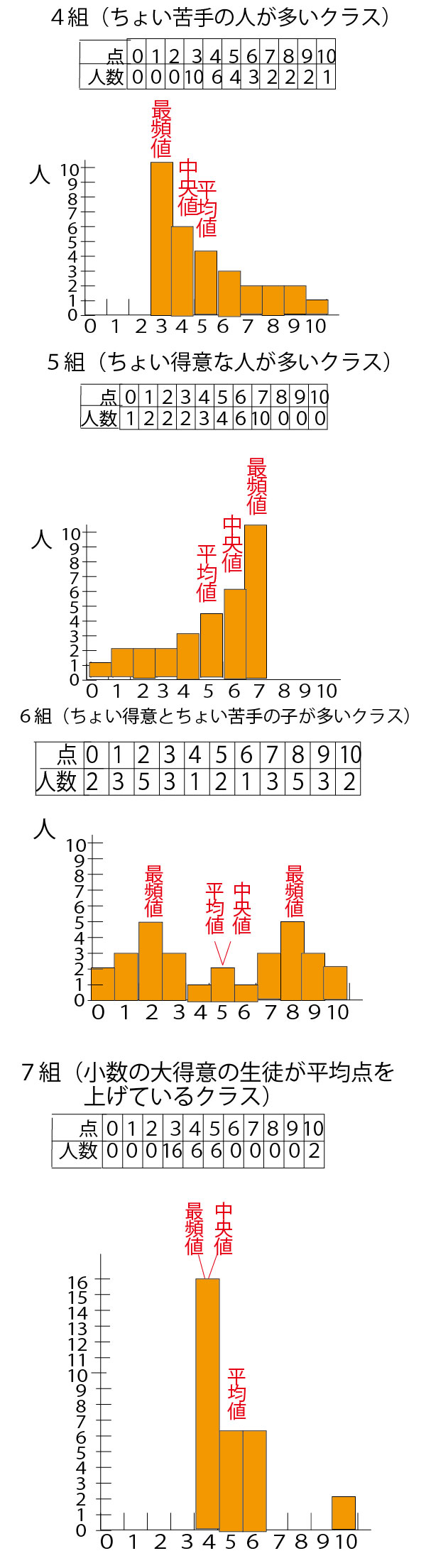


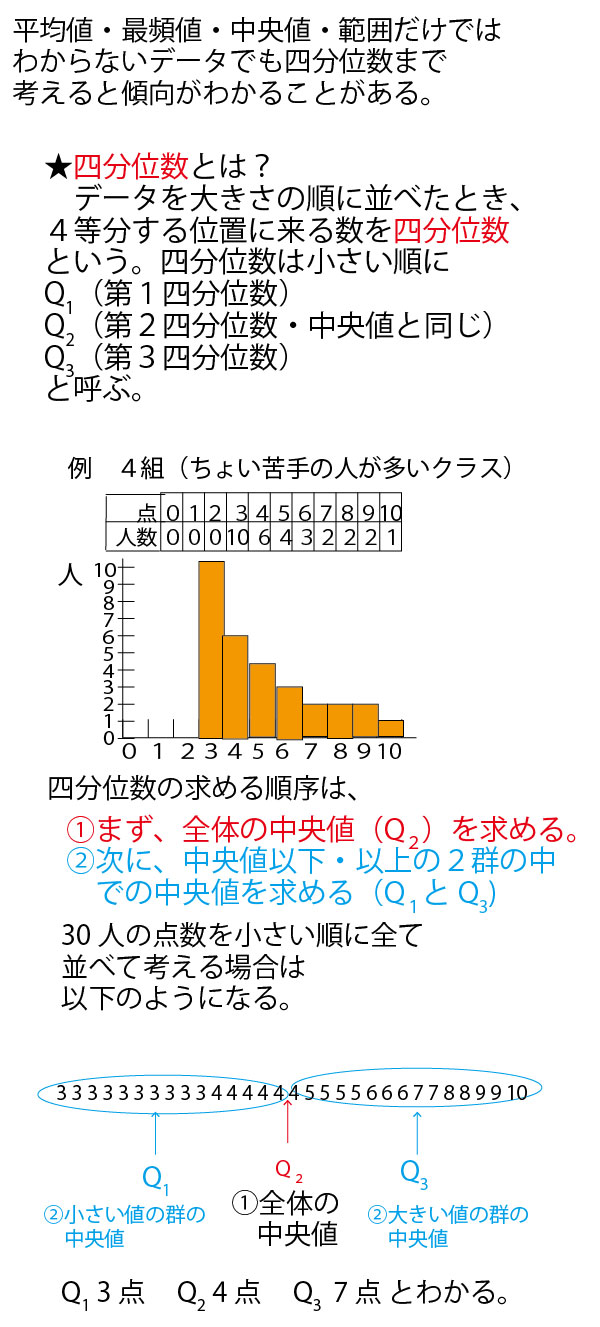




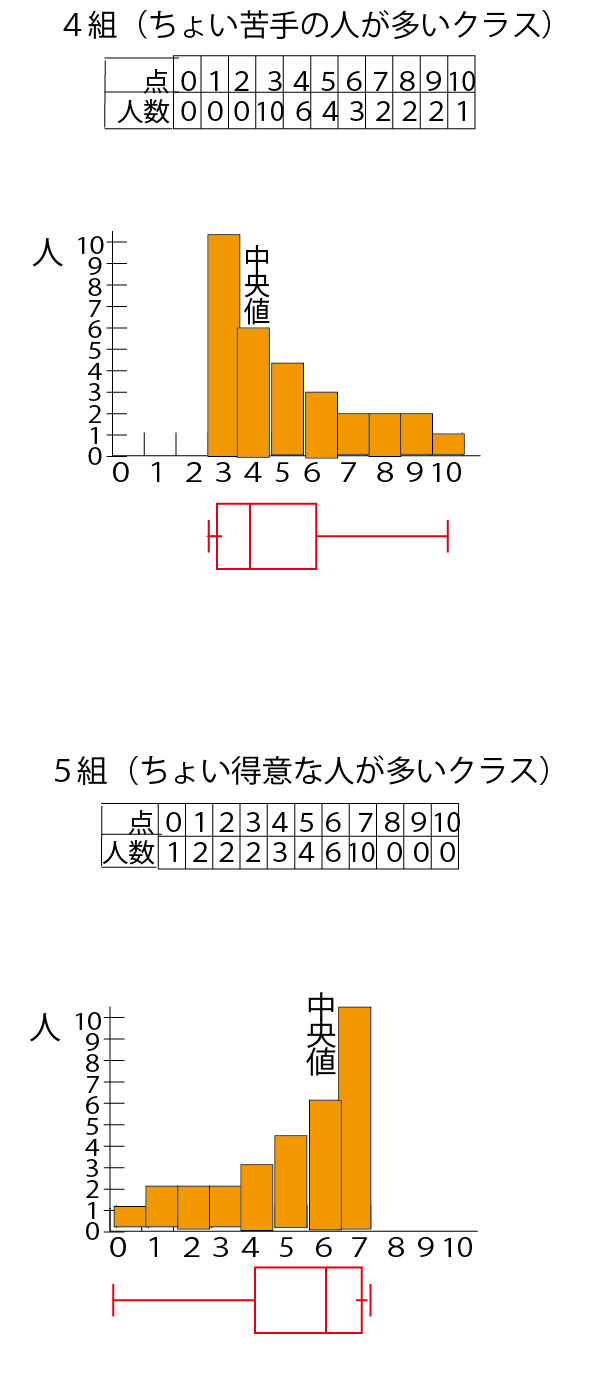
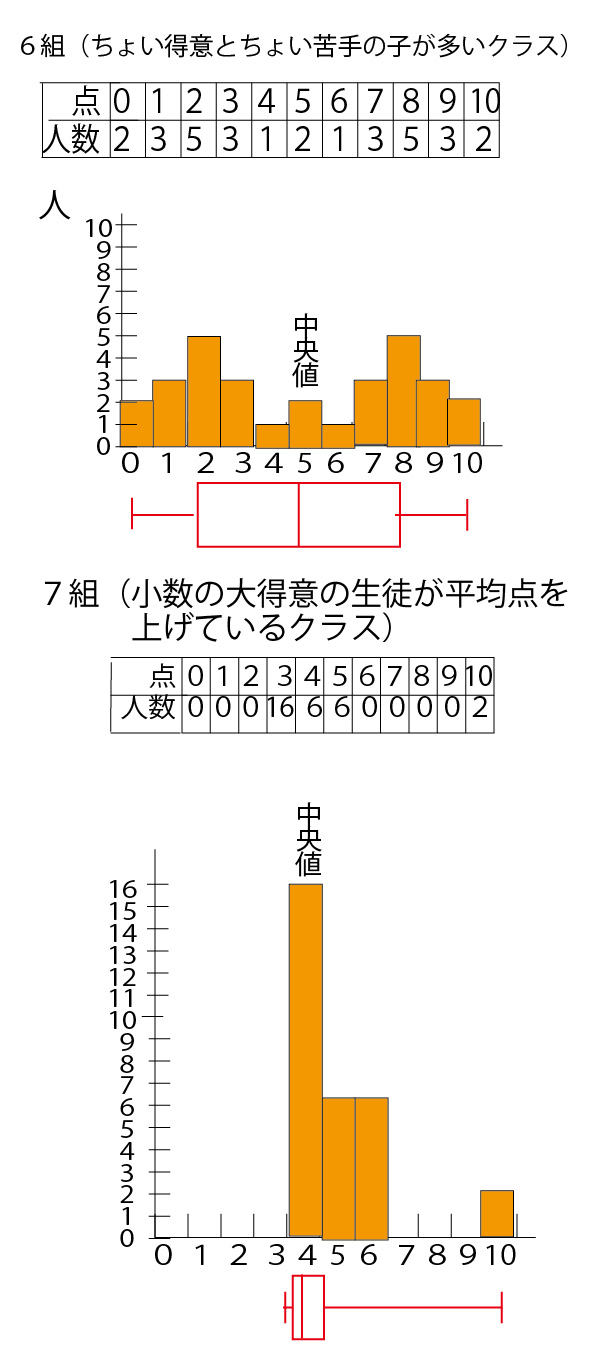
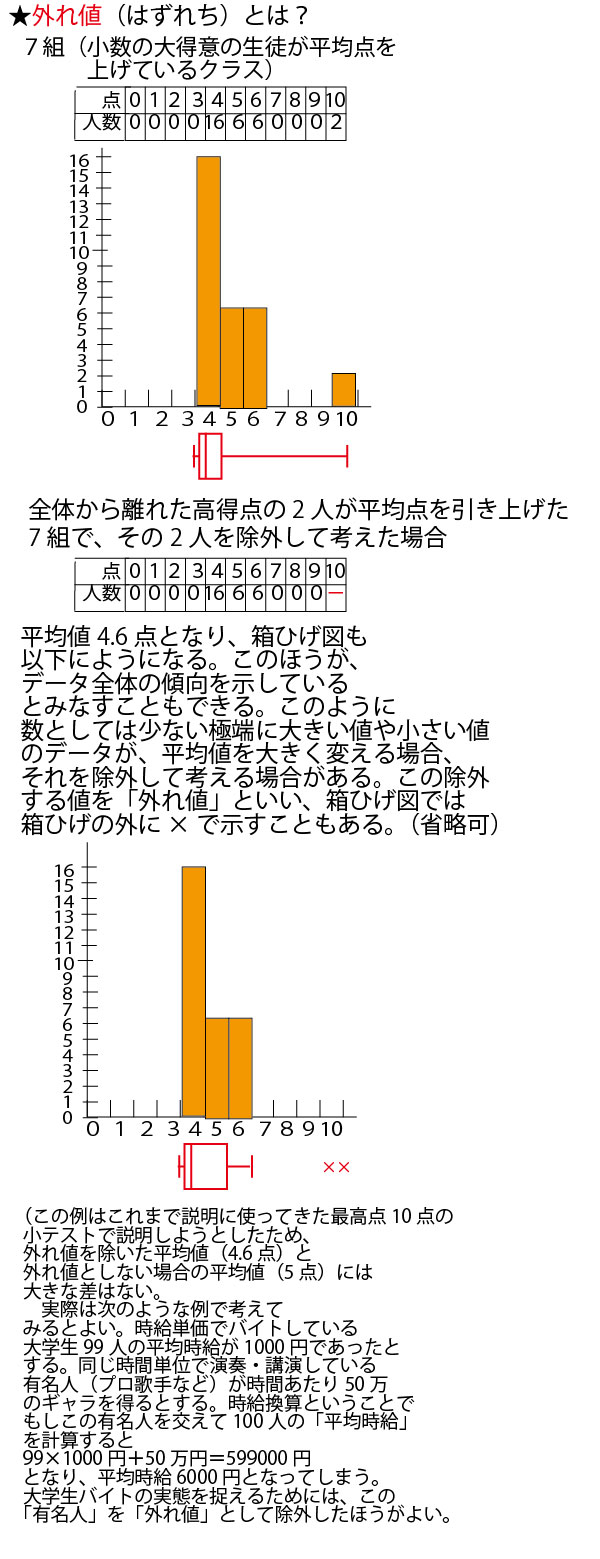

分散・標準偏差に関しては、最初に考えるのは30人クラスでは大きすぎて考えにくいので、まずは、平均点がいずれも5点となる5人組の5班(1班~5班)を例に考えていこう。