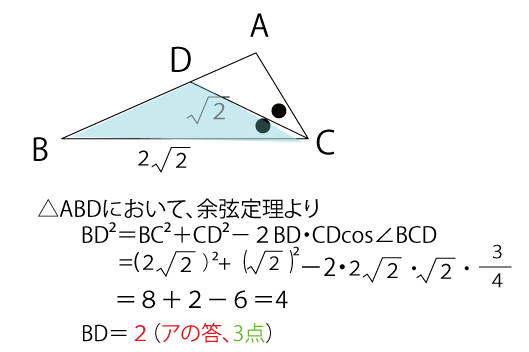
2020年大学入試センター試験「数学IA」第2問［１］（配点15点）、問題・解答・解説
asakura
解説
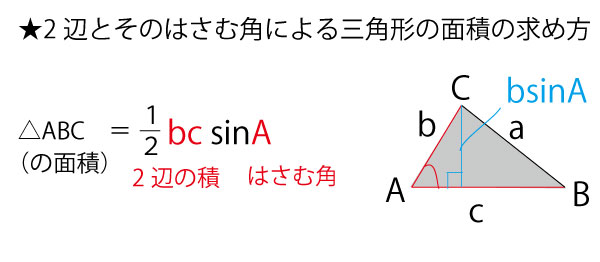
●三角比基礎事項のまとめ（一部数ⅡB含む）
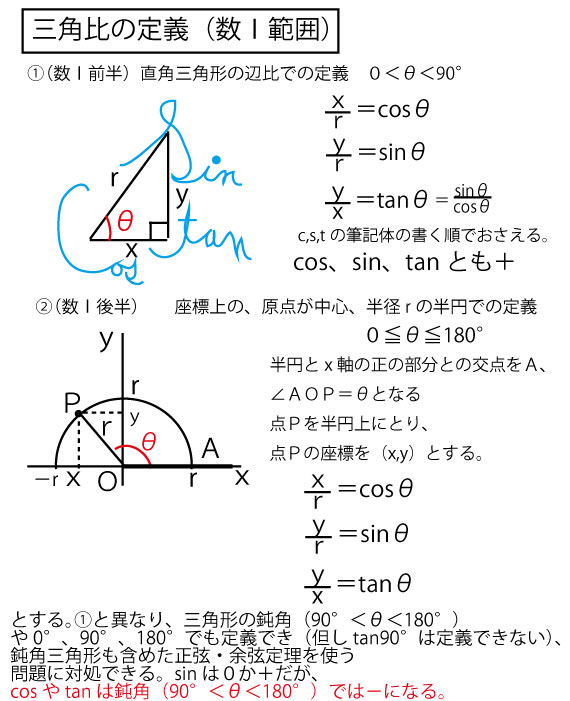
次に三角比（数Ⅱ以降は三角関数）や角の定義が高校数学で数１前半→数１後半→数２と変化する流れを理解してほしい。本問題は数１であるが、次に示した数２の基本線を知っておいたほうが解きやすい。まずはそれを説明した上で問題を解いていこう。
高校数学では角をθ（シータ）で示すことが多い。数Ⅰも最初はcos、sin、tanの定義は「直角三角形の１つの鋭角」（０＜θ＜90°）の周りの辺比に注目するという三角形に縛られた定義である。しかし、後半の定義では、直角三角形（の１つの鋭角）に縛られず、鈍角（90°＜θ＜180°）でも定義できるようになる。
次に、数２範囲での三角関数（三角比を拡大して把握したもの）の理解の初歩とその前提としての角の捉え方の変化を教えておこう。
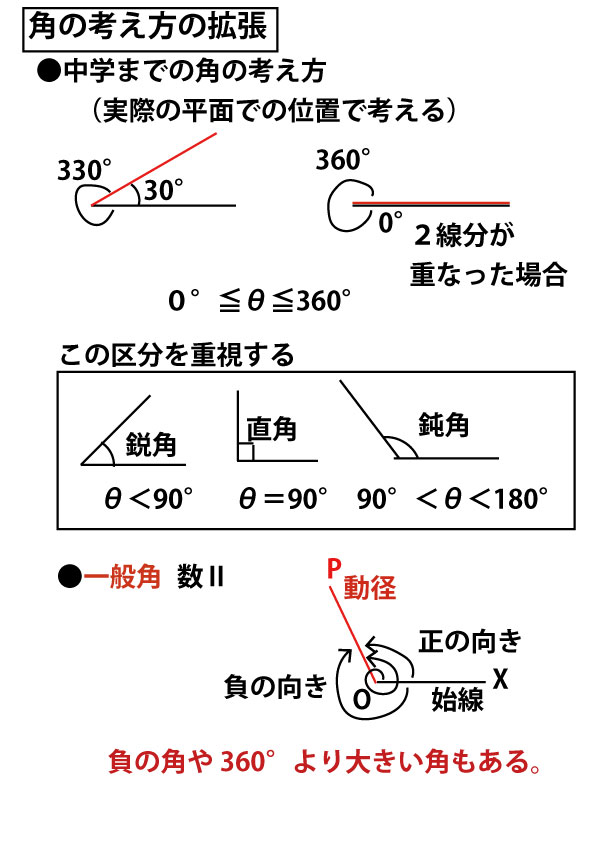
高校の数２においては、基準となる半直線OX（始線）、半直線OPをOの周りに回転させたときの角が角の定義となる。反時計回りを「正の角」、時計回りを「負の角」とし、1回転以上に回転させることも可能なので、360°以上の角もありうる。たとえば480°の角とは360°＋120°なので、実質は120°の角と同じことになる。負の角や360°を超える角も可能となるこの定義を「一般角」とい
う。さて、この一般角に角の考え方を拡張した場合の、cos、sin、tanはどう定義するのか？
数２においては、単位円（座標上で原点を中心とする半径１の円）と角θの動径の交点で定義する。（単位円の考え方は数１でも少し紹介されているが、本格的に活用するのは数２である）
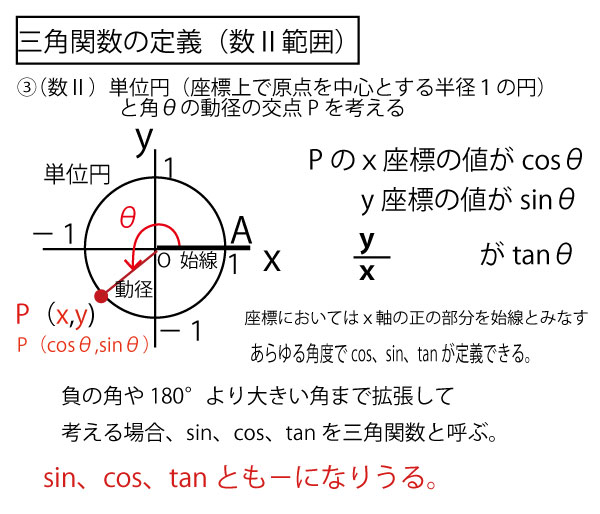
このように、ＯＰ（長さ１）が原点Ｏを中心に回転し、Ｐが単位円の円周上をθ回転した時、Ｐのｘ座標、ｙ座標が、cosθ、sinθと考えられる。この場合、角は負の角や180°より大きい角でも定義できるので、cos、sin、tanをもともと三角形の辺比の意味する「三角比」から「三角関数」と表現する。何回転しても角の定義ができることは、特に物体・天体・機械における回転運動、そして、回転運動の視野で考えると分析しやすい波の運動や往復運動などを考えやすくなり、数学が自然科学一般に応用しやすくなる。
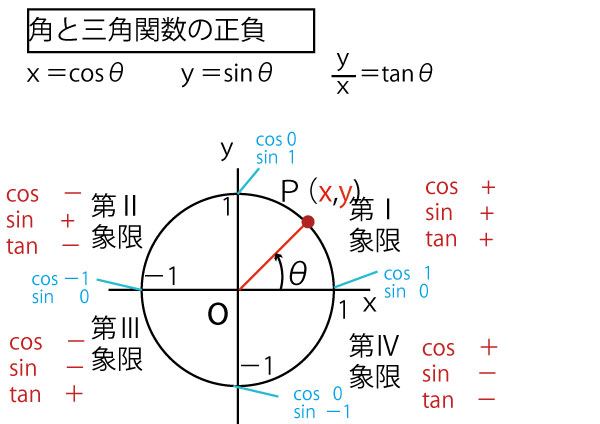
次にこの拡張したsin、cos、tanの正負を考えてみよう。数１ではとくに180°より大きい角は聞かれず、数２で本格的には使うものであるが、イメージだけでも持っておくと、数１を解くバックグランンドとなる。青字で書いた０°・90°・180°・270°の節目のcos、sinの値にも注目しておいてほしい。（とりわけ数１では、cos90°＝０、sin90°＝１は知っておきたい）
数１では鈍角（90°＜θ＜180°）に関連して、θに対し（180°ーθ）のcos、sin、tanの値がどうなるかを聞かれることが多いので、単位円の上半分の半円で考えて、以下の関係は把握しておきたい。
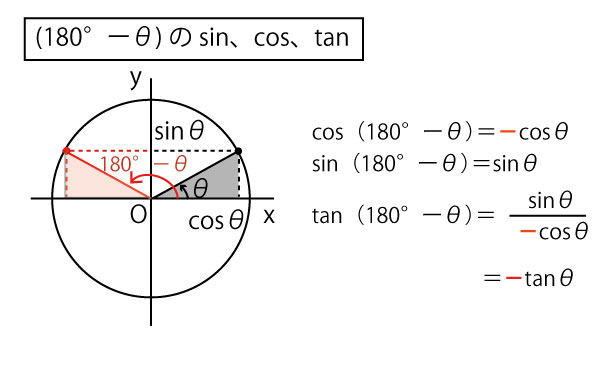
θを考えた灰色の三角形をｙ軸に関して折り返した赤の三角形が（180°ーθ）を考えるヒントとする。灰色三角形と赤三角形は合同なので辺の長さは同じで、座標上の位置で正負のみが変換しうる。cos（x座標）は正負が逆転するが、sin（y座標）は正負は逆転しない。
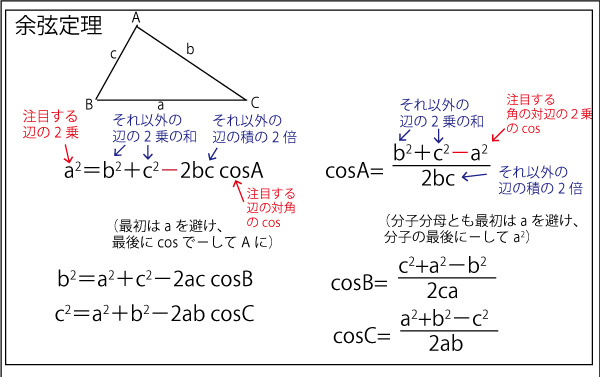
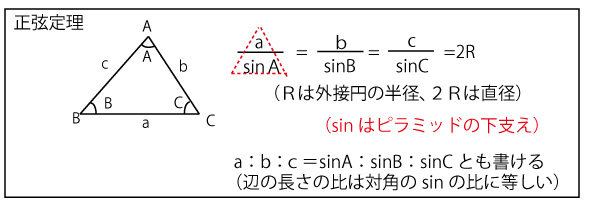
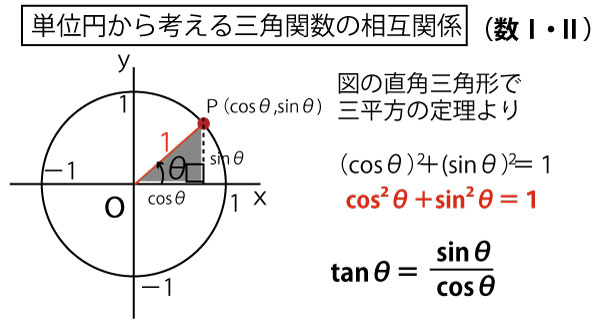
また、単位円におけるcos、sin、tanの定義から以下の三角関数の相互関係が成り立つ。
(cosθ）2、（sinθ）2、(tanθ）2は、cos2θ、sin2θ、tan2θと表記するのは一般的な表記法とされている。
ここから問題を解いてみる。
次にsinを活用した三角形の面積の求め方を確認しよう。
