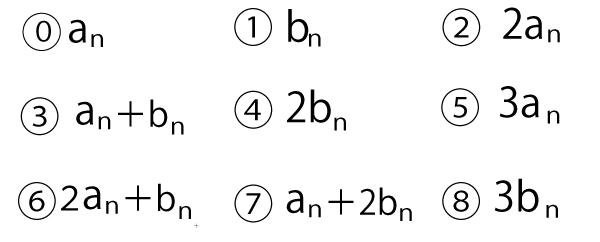2022年共通テスト「数学ⅡB」第4問（数列）問題・解答・解説

2022年5月12日　予備校講師・船橋市議　朝倉幹晴

共通テストの出題図は黒印刷ですが、せっかくの画面上ですので一部カラーといたしました。

2022年ⅡB第4問（配点20点）

以下のように、歩行者と自転車が自宅を出発して移動と停止を繰り返している。歩行者と自転車の動きについて、数学的に考えてみよう。
自宅を原点とする数直線を考え、歩行者と自転車をその数直線上を動く点とみなす。数直線上の点の座標がｙであるとき、その点は位置ｙにあるということにすえる。また、歩行者が自宅を出発してからｘ分経過した時点を時刻ｘと表す。歩行者は時刻０に自宅を出発し、正の向きに毎分１のはやさで歩き始める。自転車は時刻２に自宅を出発し、毎分２の速さで歩行者を追いかける。自転車が歩行者に追いつくと、歩行者と自転車はともに1分だけ停止する。その後、歩行者は再び正の向きに毎分１の速さで歩き出し、自転車は毎分２の速さで自宅に戻る。自転車は自宅に到着すると、1分だけ停止した後、再び毎分２の速さで歩行者を追いかける。これを繰り返し、自転車は自宅と歩行者の間を往復する。
ｘ＝a_nを自転車がｎ回後に自宅を出発する時刻とし、ｙ＝b_nをそのときの歩行者の位置とする。

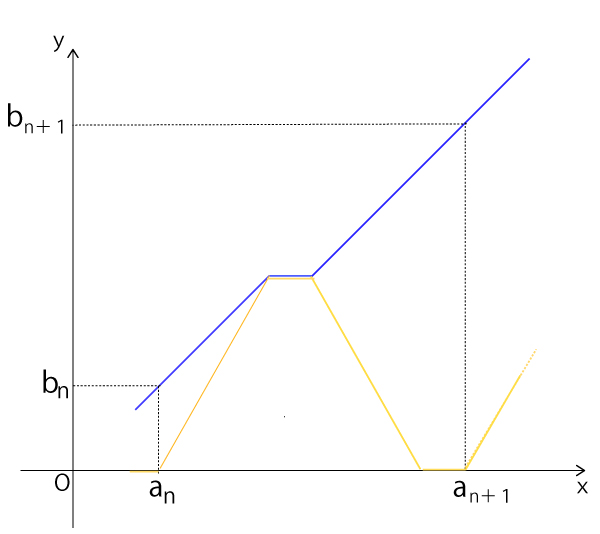
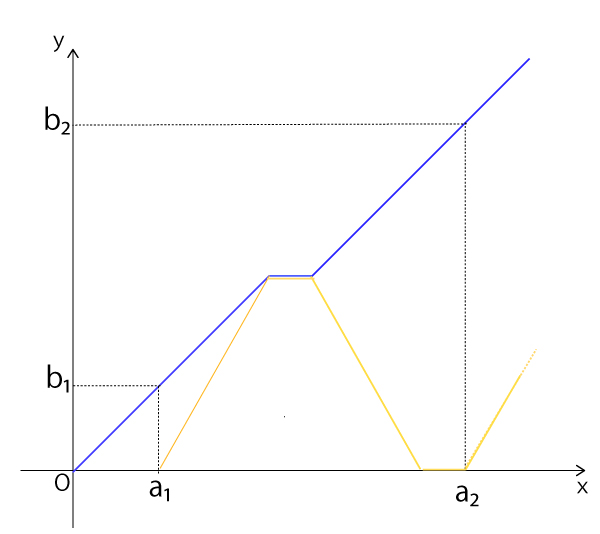
（1）花子さんと太郎さんは、数列{a_n}、{b_n}の一般項を求めるために、歩行者と自転車について、時刻ｘにいて位置ｙにいることをＯを原点とする座標平面上の点（x,y)で表すことにした。

a₁＝2、b₁＝2により、自転車が最初に自宅を出発するときの時刻と自転車の位置を表す点の座標は（2,0)であり、そのときの時刻と歩行者の位置を表す点の座標は（2,2)である。また、自転車が最初に歩行者に追いつくときの時刻と位置を表す点の座標は（ア,ア）である。よって
a₂＝イ、b₂＝ウ
である。

花子：数列{a_n}、{b_n}の一般項について考える前に、（ア,ア）の求め方について整理してみようか。
太郎：花子さんはどうやって求めたの？
花子：自転車が歩行者を追いかけるときに、間隔が１分間に１つずつ縮まっていくことを利用したよ。
太郎：歩行者と自転車の動きをそれぞれ直線の方程式で表して、交点を計算して求めることもできるね。

自転車がｎ回目に自宅を出発するときの時刻と自転車の位置を表す点の座標は（a_n,0)であり、そのときの時刻と歩行者の位置を表す点の座標（a_n,b_n)である。よって、n回目に自宅を出発した自転車が次に歩行者に追いつくときの時刻と位置を表す点の座標は、a_n,b_nを用いて、（エ、オ）と表せる。

エ、オの解答群（同じものを繰り返し選んでもよい。）

以上から、数列{a_n}、{b_n}について、自然数ｎに対して、関連式
a_n+1＝a_n＋カ_bn＋キ　……
b_n+1＝3b_n+ク　　……
が成り立つことがわかる。まず、b₁＝２とから

b_n＝ケ（ｎ＝1,2,3,‥‥）
を得る。この結果と、a₁＝2およびから
a_n＝コ（ｎ＝1,2,3,‥‥）
がわかる。
ケ、コの解答群（同じものを繰り返し選んでもよい。）

（2）歩行者がｙ＝300の位置に到着するときまでに、自転車が歩行者に追いつく回数はサ回である。また、サ回目に自転車が歩行者に追いつく時刻は、ｘ＝シスセである。

[next_p]