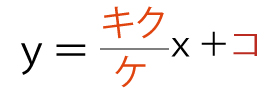2019センター数ⅡB「円と直線」センター追試第1問[１]「円と直線の方程式」問題・解答・解説（15点配点）

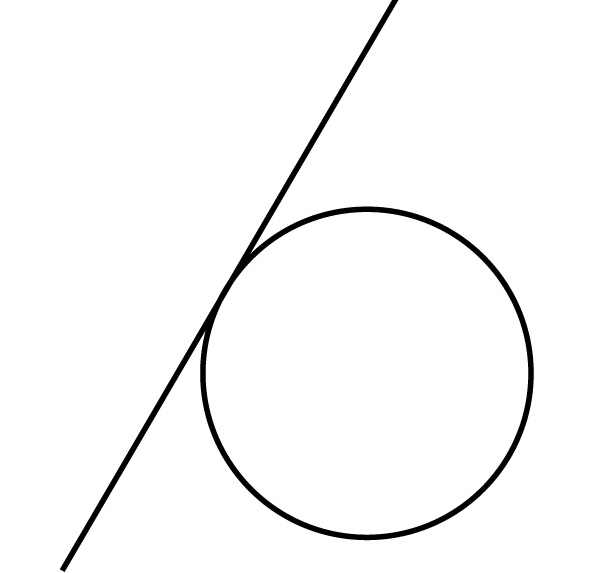
2022年5月19日　予備校講師・船橋市議（無党派）　朝倉幹晴

2019年大学入試センター数学ⅡB追試第2問［１］の問題・解答・解説です。入試問題はカラーですが、せっかくの画面上ですので一部カラーにしました。ご活用ください。

第1問[１]aを実数とする。座標平面上で、点（3.1)を中心とする半径１の円をCとし、直線ｙ＝axをℓとする。

（1）円Cの方程式は
x²＋y²−アｘーイｙ＋ウ＝０（アイウ、合わせて２点）
である。
（2）円Cと直線ℓが接するのは

（エ1点、オカ2点）

のときである。
のとき、Cとℓの接点を通り、ℓに垂直な直線の方程式は

（キクケ合わせて2点、コ2点）

である。ただし、キク、ケ、コは、文字aを用いない形で答えること。

（3）円Cと直線ℓが異なる2点A、Bで交わるとき、二つの交点を結ぶ線分ABの長さは

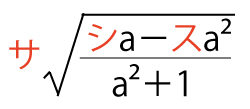
（サシス合わせて4点）

である。また、ABの長さが２となるのは

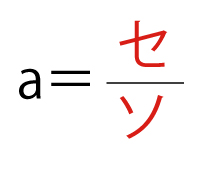
（セソ合わせて2点）

のときである。
[next_p]