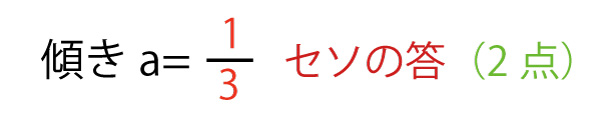2019センター数ⅡB「円と直線」センター追試第1問[１]「円と直線の方程式」問題・解答・解説（15点配点）

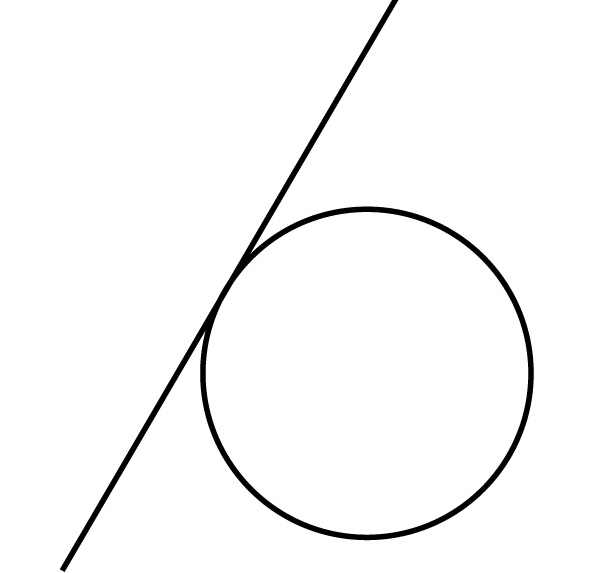
解説

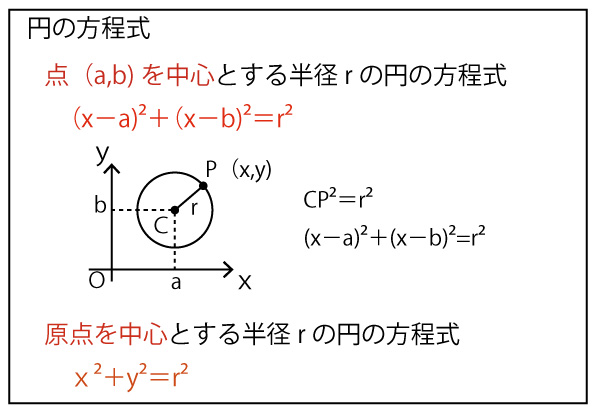
（1）（3,1)を中心とし、半径1の円Cの方程式は
（ｘ－3)²＋（ｙ－1）²＝１²
　　　ｘ²−6x＋9＋y²−2y＋１＝１
　　ｘ²＋y²−6（ア）x－2（イ）y＋９（ウ）＝0（アイウ合わせて2点）

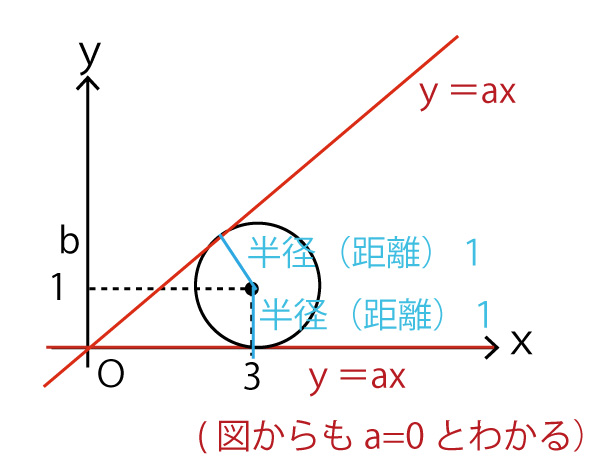
（2）円Cと直線ℓが接するのは、点（3,1)とｙ＝axつまりax−y+0＝０の距離が１の時なので

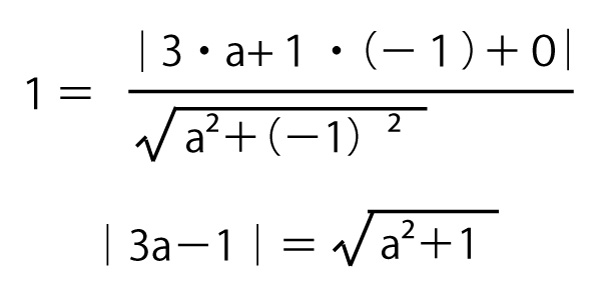
両辺を二乗して
（3a－1）²＝a²＋１
9a²−6a＋１＝a²+1
8a²−6a=0
4a²−3a=0
a(4a－3)=0

のとき、Cとℓの接点を通り、ℓに垂直な直線の方程式を求めるために
まず、接点を求める。

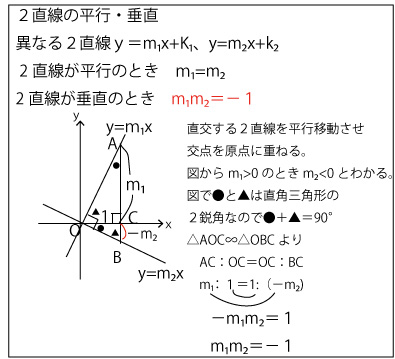
（3）円Cと直線ℓが異なる2点で交わるときは、以下のような図となる。

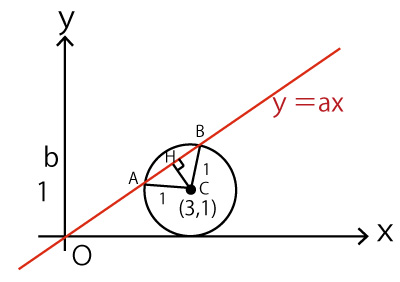
円Cの中心をCとし、Ｃからℓに下ろした垂線の足をＨとする。AC＝１、CB＝１。
CHは点C(3,1)とｙ＝axの距離なので

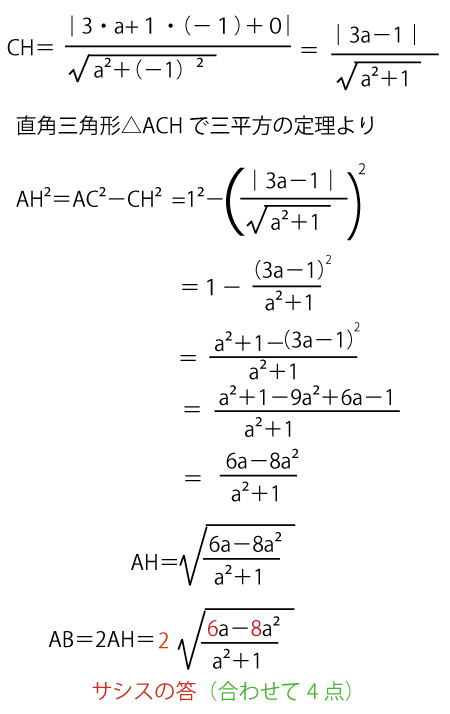
AB＝２の時は、ABは円Cの直径なので、ℓは円の中心（3.1)を通る。よって