2014年大学入試センター「数学」ⅡB第1問［１］「図形と方程式」（配点15点）問題、解答・解説
asakura
2022年6月8日 予備校講師・船橋市議（無党派） 朝倉幹晴
2014年の大学入試センター「数学」ⅡB第1問［１］「図形と方程式」の解答解説を作りましたので、勉強、入試対策にご活用ください。
第1問［１］（配点15点）
Oを原点とする座標平面において、点P（p,q)を中心とする円Cが、方程式
で表される直線ℓに接しているとする。
（1）円Cの半径rを求めよう。
点Pを通り直線ℓに垂直な直線の方程式は
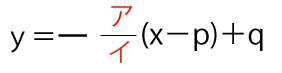
なので、Pからℓに引いた垂線とℓの交点Qの座標は
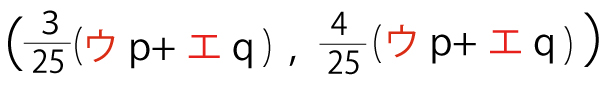
となる。
求めるCの半径rは、Pとℓの距離PQに等しいので
である。
（2）円Cが、ｘ軸に接し、点Ｒ（2,2)を通る場合を考える。このとき、ｐ＞０、ｑ＞0である。Ｃの方程式を求めよう。
Ｃはｘ軸に接するので、Ｃの半径ｒはqに等しい。したがって、
により、ｐ＝キqである。
Cは点Rを通るので、求めるCの方程式は
（ｘ－ク）2＋（y－ケ）2＝コ…
または
（ｘ－サ）2＋（y－シ）2＝ス…
であることがわかる。ただし、コ＜スとする。
（3）方程式の表す円の中心をS、方程式
の表す円の中心をTとおくと、直線STは原点Oを通り、点Oは線分STをセする。セに当てはまるものを、次の
のうちから一つ選べ。
１：１に内分 １：２に内分 2：1に内分
１：１に外分 
１：２に外分 
２：１に外分
[next_p]
