2019年大学入試センター試験数学ⅡB第1問［１］（三角関数、配点15点）問題、解答、解説

関数ｆ（θ）＝3sin²θ＋4sinθcosθーcos²θを考える。

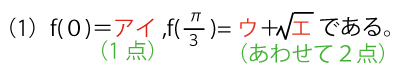
（2）2倍角の公式を用いて計算すると、

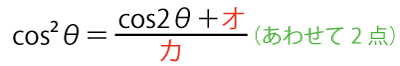
となる。さらに、sin２θ、cos２θを用いてｆ（θ）を表すと
ｆ（θ）＝キsin2θ－クcos2θ＋ケ‥‥（キクケあわせて3点）

となる。

（3）θが０≦θ≦π（パイ）の範囲を動くとき。関数ｆ（θ）のとり得る最大の整数の値ｍとそのときのθの値を求めよう。
三角関数の合成を用いるとは

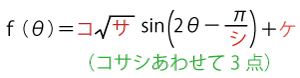
と変形できる。したがって、ｍ＝ス（2点）である。
また、０≦θ≦π（パイ）において、ｆ（θ）＝スとなるθの値は、小さい順に、

である。

[next_p]