2021年共通テスト（第2日程）第1問[１]（指数・対数、配点15点）問題・解答・解説

目次

Toggle

2021年共通テスト数学ⅡB（第２日程）第1問解答（計13点）
ア１（1点）　イlog₁₀2＋ウ　ーlog₁₀2＋１（2点）  エlog₁₀2+log₁₀3+オ  －log₁₀2+log₁₀3+１（2点）
カキ　23（2点）　　クケ 24（2点）　  log₁₀コ　log₁₀３（2点） サ３（2点）

［解説］

（1）log₁₀10＝ア（1）（1点）

である。
また、log₁₀5、log₁₀15をそれぞれlog₁₀2とlog₁₀3を用いて表すと

log₁₀5＝イlog₁₀2＋ウ     
log₁₀5＝log₁₀10／2＝log₁₀10ーlog₁₀2＝－log₁₀2＋1（イウの答、2点）

log₁₀15＝エlog₁₀2+log₁₀3+オ
log₁₀15＝log₁₀5・3＝log₁₀5＋log₁₀3
＝（－log₁₀2＋1）＋log₁₀3＝－log₁₀2＋log₁₀3＋1（エオの答、2点）

（2）太郎さんと花子さんは15²⁰について話している。
以下では,log₁₀2＝0.3010、log₁₀3＝0.4771とする。

太郎：15²⁰は何桁の数だろう。
花子：15の20乗を求めるのは大変だね。
log₁₀15²⁰の整数部分に着目してみようよ。

log₁₀15²⁰は
log₁₀15²⁰＝20log₁₀15＝20（1＋log₁₀3ーlog₁₀2)
=20 ×（１＋0.4771ー0.3010)
=20×1.1761＝23.522
カキ(23)＜log₁₀15²⁰＜カキ(23)＋１　（カキ2点）
を満たす。よって、15²⁰はクケ(24)桁の数である。（クケ2点)

太郎：15²⁰の最高位の数字も知りたいね。
だけど、log₁₀15²⁰の整数部分にだけ着目してもわからないね。
花子：Ｎ・10^{カキ（23）}＜15²⁰＜（N+1）・10^{カキ（23）}を満たすような
正の整数Ｎに着目してみたらどうかな。

log₁₀15²⁰の小数部分はlog₁₀15²⁰−カキ（23）であり
15²⁰＝x・10²³とすると
log₁₀15²⁰＝log（x・10²³）＝23＋log₁₀X＝23.522
log₁₀X=0.522

Ｎ・10²³＜15²⁰＜（N+1）・10²³　なので
log₁₀(Ｎ・10²³)＜log₁₀15²⁰＜log₁₀［（N+1）・10²³］
23＋log₁₀N＜23＋log₁₀X<23+log₁₀(N+1)
log₁₀N＜log₁₀X＜log₁₀(N+1)

log₁₀コ(N)＜log₁₀15²⁰－カキ（23）＜log₁₀(コ(N)＋1）
が成り立つ。
つまり
log₁₀コ(N)＜log₁₀X＜log₁₀(コ(N)＋1）が成り立つ。
したがって
log₁₀コ(N)＜0.522＜log₁₀(コ(N)＋1）

log₁₀4＝log₁₀2²＝2log₁₀2＝2×0.3010＝0.6020
log₁₀3＝0.3010
0.3010＜0.522<0.6020

log₁₀コ（3）＜0.522＜log₁₀(コ（3）＋1）（コ2点)

15²⁰の最高位の数字はサ（3）である。（サ2点)

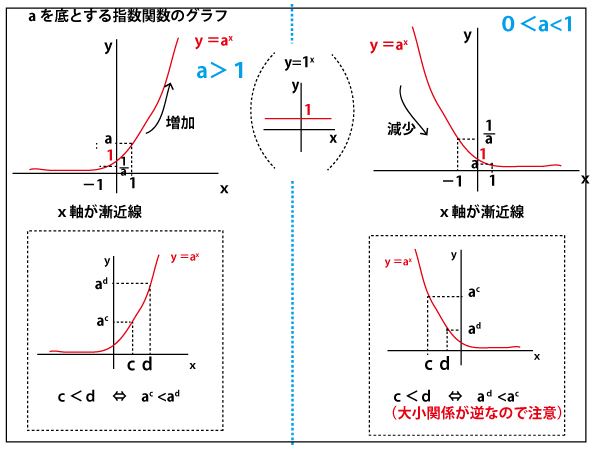
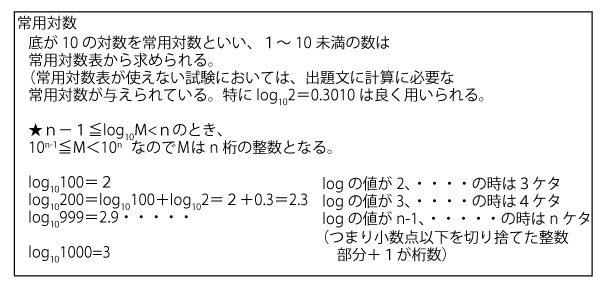
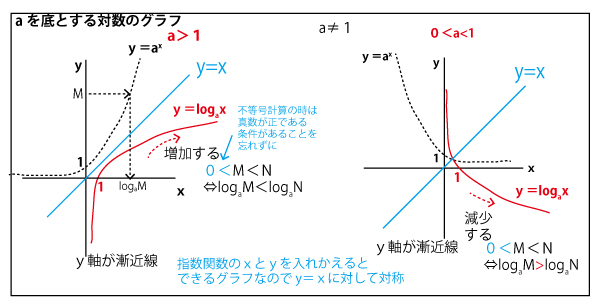
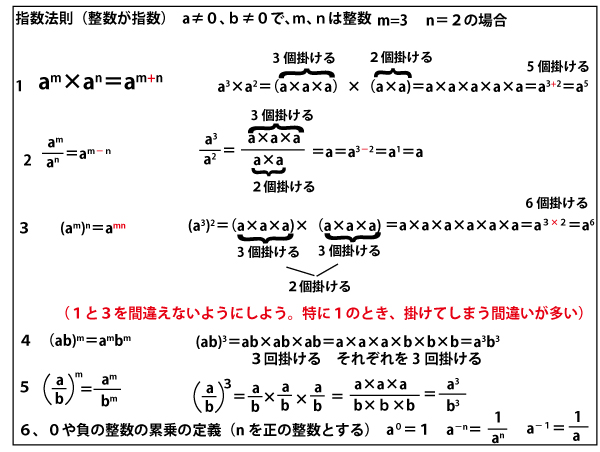
＜指数関数・対数関数の基本＞