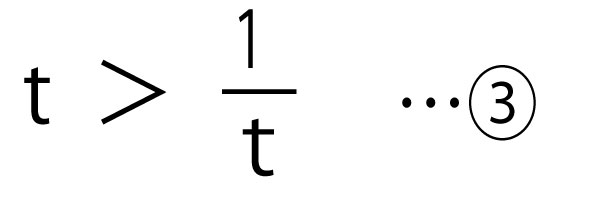2022年大学入試共通テスト数学ⅡB第１問[２]（指数・対数）（配点15点）問題・解答・解説

2022年7月4日 2022年7月4日

asakura

2022年7月　予備校講師・船橋市議　朝倉幹晴

2022年大学入試共通テスト数学ⅡB第１問[１]（指数・対数）（配点15点）の解答・解説を作成しました。復習に役立ててください。

（3）次に、太郎さんは（2）の考察をもとにして

を満たす実数ｔ（ｔ≠0）の値の範囲を求めた。

太郎さんの考察
ｔ＞０ならば、の両辺にｔを掛けることにより、t²＞１を得る。このようなｔ（ｔ＞0）の値の範囲は１＜ｔである。
ｔ＜０ならば、、の両辺にｔを掛けることにより、t²＜１を得る。このようなｔ（ｔ＜0）の値の範囲は－１＜ｔ＜０である。

この考察により、を満たすｔ（ｔ≠０）の値の範囲は
－１＜ｔ＜０、１＜ｔ
であることがわかる。
ここでaの値を一つ定めたとき、不等式

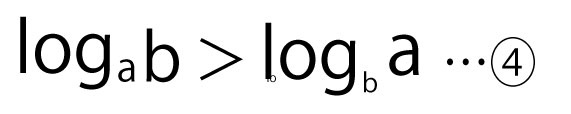
を満たす実数ｂ（ｂ＞０、ｂ≠１）の値の範囲について考える。
を満たすｂの値の範囲は、a＞１のときはチ（2点）であり、０＜a＜1のときはツ（2点）である。