2022年千葉県公立高校入試「数学」第1問（4）（数と式・確率）問題、解答、解説（計6点）

【解説】
素数は、1とそれ自身以外に約数を持たない2以上の自然数（１は素数に含めない）である。２以外は全て奇数である。
２、３、５、７、11、13、17、19の8個。

素数ではない数の約数　１（１）、４（１、２、４）、６（１，２、３、６）、８（１，２，４，８）、９（１、３、９）、10（１，２、５、10）、12（１、２、３、４、６、12）、14（1，2，7，14）、15（1，3，5，15）、16（1，2，4，8，16）
18（1，2，3，6，9，18）、20（1，2，4，5，10、20）

小さいさいころの出る目（a)の場合の数は１～６の6通り、大きいさいころの出る(b)目の数も１～６の６通り。
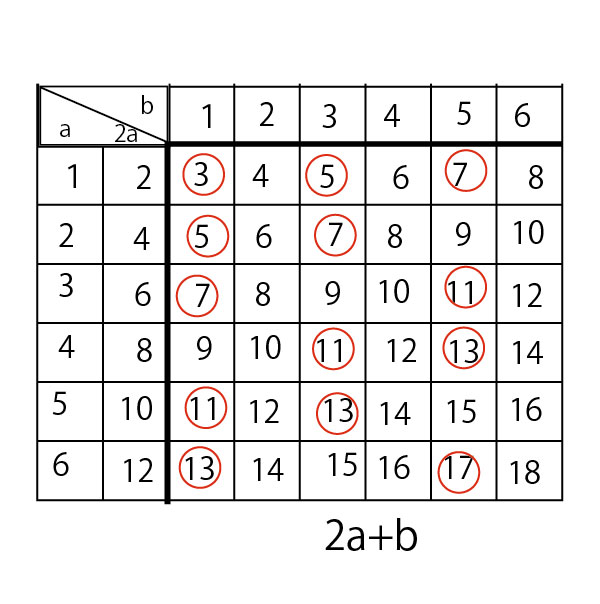
両方のさいころを同時に投げた時の目の場合の数は６×６＝36通り。そこで2a+bは以下の表のようになる。36のマスの中で、素数になるのは13コマで、、確率は13／36。
千葉県でよく出題されるさいころ２つの確率の問題はこの36マスの碁盤目を書いてその中で条件にあてはまるマスを〇で囲み、その〇の数を数え、場合の数36で割ると確率を求めることができる。