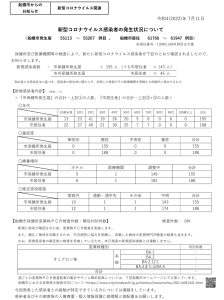
2022年千葉県公立高校入試「数学」第４問問題、解答、解説（計18点）

2022年7月　予備校講師・船橋市議　朝倉幹晴

2022年2月に実施された千葉県公立高校入試「数学」第4問（計18点）の解答・解説を作成しました。また千葉県教育委員会が発表した正答率・無答率も付記しました。学習や入試対策にご活用ください。

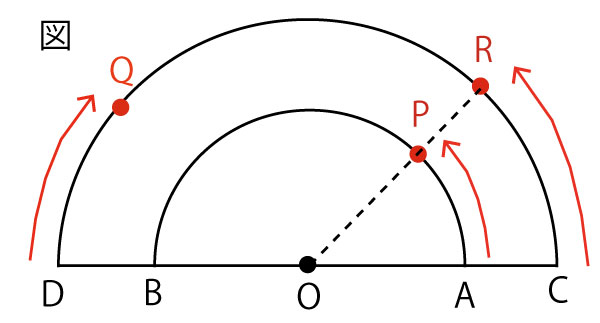
図のように、点Oを中心と市、線分AB、CDを直径とする２つの半円がある。
点PはAを、点QはDを同時に出発する。Aを出発した点Pは、上を一定の速さで移動し、→Ｂ→A→B→Ａ→・・・・・・・の動きをくり返す。
Ｄを出発した点Ｑは、上を一定の速さで移動し、→Ｃ→Ｄ→Ｃ→Ｄ→・・・・・・・の動きをくり返す。
＝60cm、＝90cm、2点P、Qの移動する速さを、それぞれ秒速4cm、秒速9cmとするとき、あとの（1）～（5）の問いに答えなさい。（計18点）

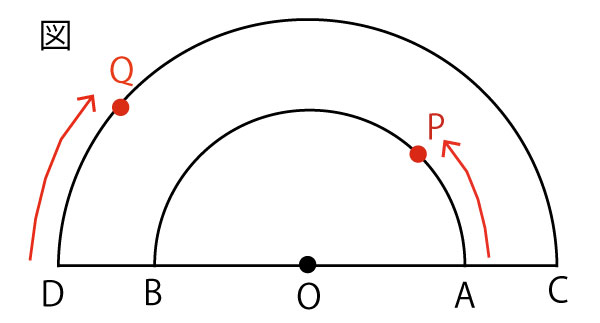
会話文
牧師T：3点O、P、Qが、この順に一直線上に並ぶ場合について考えます。点PがAを、点QがDを同時に出発してからｘ秒後の2点Ｐ、Ｑの位置関係を確認してみましょう。
生徒Ｘ：点Ｐの動きについて考えてみます。
＝60cmで、点Ｐの速さが秒速4cmだから、点ＰがＡを出発してから、Ｂにはじめて到着するのは15秒後だとわかります。点Ｐが出発してから、ｘと
の長さの関係をグラフに表すと、下のようになりました。

生徒Ｙ：点Ｑの動きについて考えてみると、＝90cmで、点Qの速さが秒速9cmだから、点QがDを出発してから、Cにはじめて到着するのは（a)秒後です。
の変化のようすをグラフに表すと何がわかるかな。
生徒X：との変化のようすがわかっても、点Pと点Qは異なる円周上を動くから、3点O、P、Qが、この順に一直線上に並ぶ場合を考えるのは難しいですね。
教師Ｔ：下の図のように、直線ＯＰとの交点をＲとすると、点Ｐが上を移動する速さが秒速4cmだから、点Ｒが、上を移動する速さは秒速（b)cmだと考えることができます。

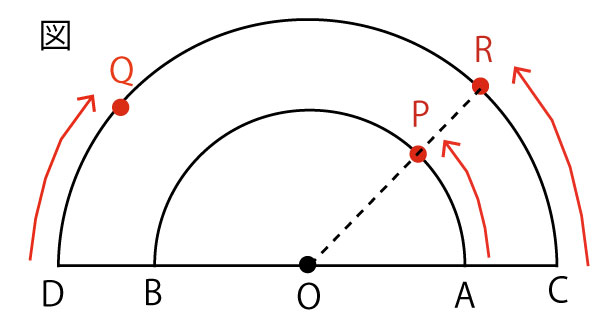
生徒Y：同じ上で、2点Q、Rの動きをみることができるので、考えやすくなりました。3点O、P、Qが、この順に一直線上に並ぶのは、のときだね。
生徒X：だから、
のときとも考えられますね。まず、の変化のようすを調べてみます。点QがDを出発してからｘ秒後の
の長さをｙcmとすると、点ＱがＣにはじめて到着するまでのｘとｙの関係を表す式は、ｙ＝90ー9xになります。

（1）会話文中の（a)(b)にあてはまる数として最も適当なものを、次のア～カのうちからそれぞれ１つずつ選び、符号で答えなさい。（３点×２＝6点）
ア４　イ６　ウ８　エ10　オ12　カ14
（a3点、正答率86.5%、無答率1,7%)（b3点、正答率57.1％、無答率4.9%)

（２）点QがDを出発してからｘ秒後のの長さをｙcmとする。０≦ｘ≦30のときのｘとｙの関係を表すグラフを書きなさい。（3点）（正答率28.9%、無答率26.8%)

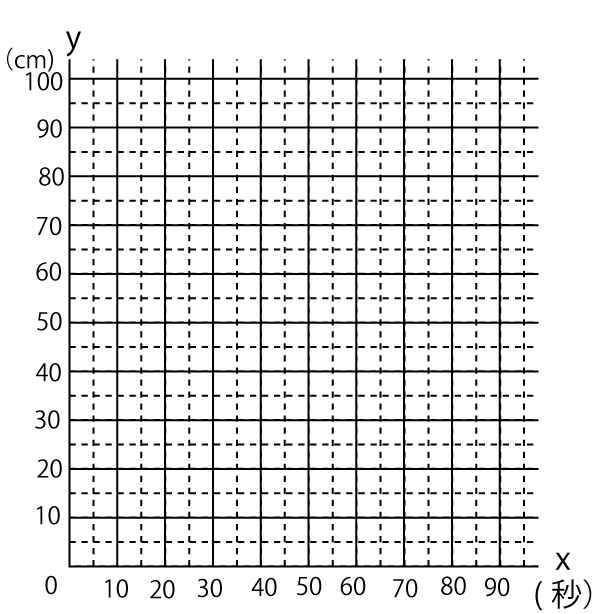
（3）点PがAを、点QがDを同時に出発してから、3点O、P、Qが、はじめてこの順に一直線上に並ぶのは何秒後か、求めなさい。（3点）（正答率17.5%、無答率26.4%)
（4）点PがAを、点QがDを同時に出発してから、点PがAに、点QがDにはじめて同時に到着した。2点P、Qが同時に出発してからこのときまでに、3点O、P、Qが、この順に一直線上に並ぶのは何回あったか、求めなさい。
                                 （3点）（正答率8.1%、無答率34.5%)
（5）点PがAを、点QがDを同時に出発してから、144秒後の∠POQの大きさを求めなさい。（3点）（正答率4.4%、無答率52.2%)
[next_p]