2022年千葉県公立高校入試「数学」第４問問題、解答、解説（計18点）

【解説】

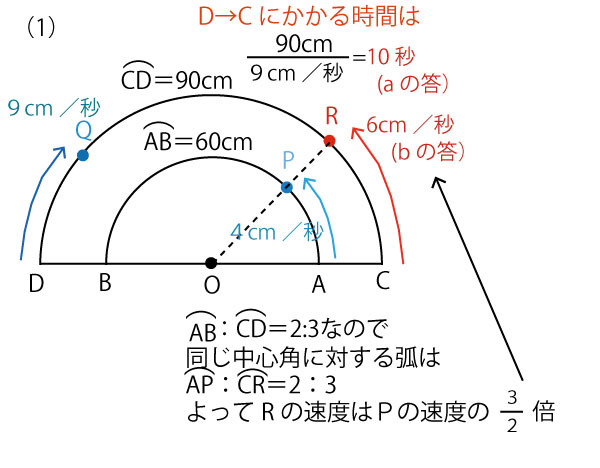
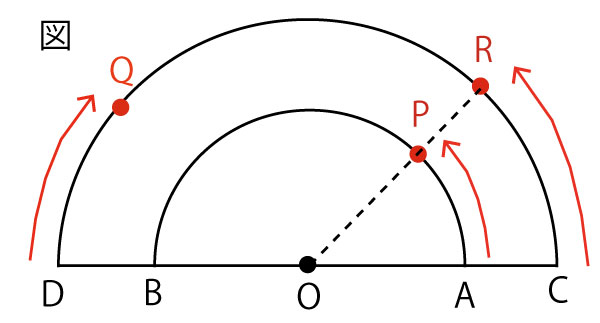
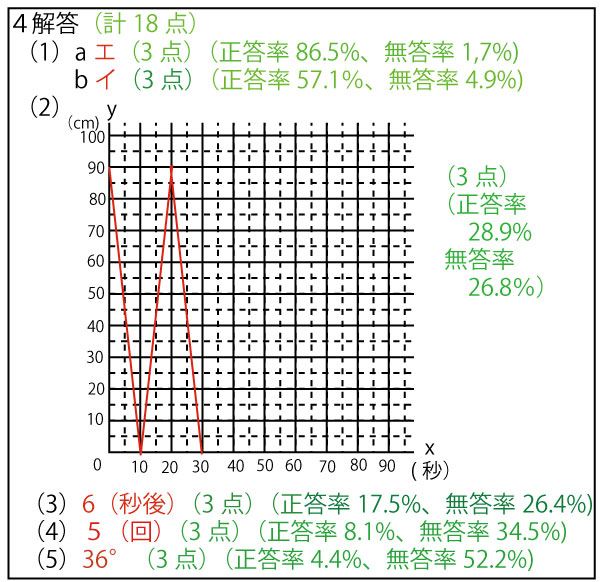
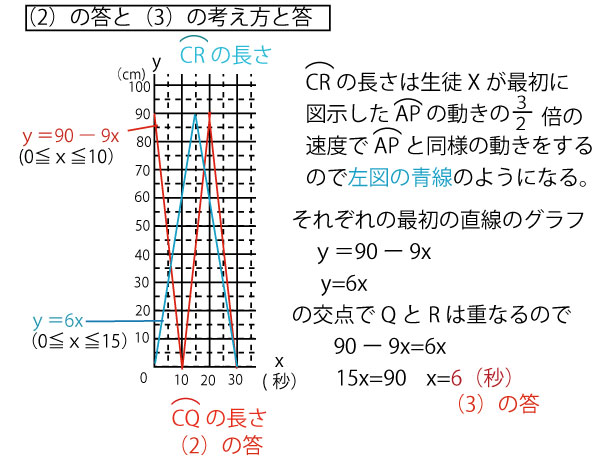
（2）（3）０秒ではDに存在し、CQ＝90cm、10秒でCに到達し、CQ＝０cmとなる。そして次の10秒（最初からは20秒目）でDに戻り再びCQ＝90cmとなる。そして次の10秒（最初からは30秒目）でCに到達し、CQ＝０cmとなる。したがって下の赤直線のようになる。として（3）は以下のように求められる。

（4）（3）では０≦ｘ≦30の範囲だけを問うているのに、出題者はｘ＝90までのグラフを描けるように問題図を与えている。つまり、この問題用紙の図を（4）以降を考える時に活用するように示唆している。
したがって、（3）を考えるために描いたグラフの続きを描き、（4）の条件（点PがAに、点QがDにはじめて同時に到達した）を求めると、60秒（下図の●）とわかり、その間に5回QとRが出会っている（つなり、3点O、P、Qがこの順に並ぶ）（下図の●）ことが確認できる。

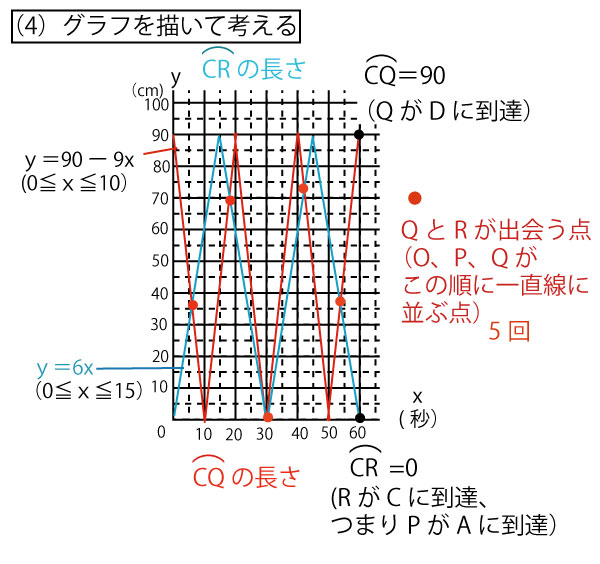
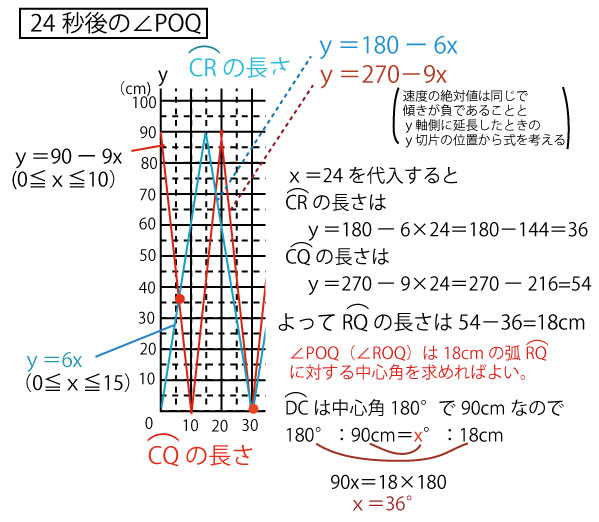
（5）上図より30秒で重なり合う（∠POQ＝∠ROQ＝0）、60秒で直径の両端に来る（∠POQ＝∠ROQ＝180°）。そしてそれが繰り返されることがわかる。
つまりｘを整数とすると、60ｘ秒のとき、∠ＰＯＱ＝180°、60ｘ＋30のとき、∠ＰＯＱ＝0°となる。
144秒＝60×２＋24なので、60×２＝120秒で、最初の状態に位置に戻ったあと、24秒目なので、上図で24秒の位置を考える。