2023年千葉県公立高校入試「数学」第1問（5）（場合の数・確率）（配点6点）問題・解答・解説

【解説】

場合の数と確率も問題は、千葉県では「大・小２つのサイコロを同時にふる」問題が多い。ただ、時々、「カードを●枚引く」場合も出題され、今回はその出題であった。わかりやすいようにカードをサイコロの目の数と同じ１～６の6枚のカードを引く場合で考えてみよう。
ただしカードは引く時の引き方、約束ごとによって場合の数は異なってくる。

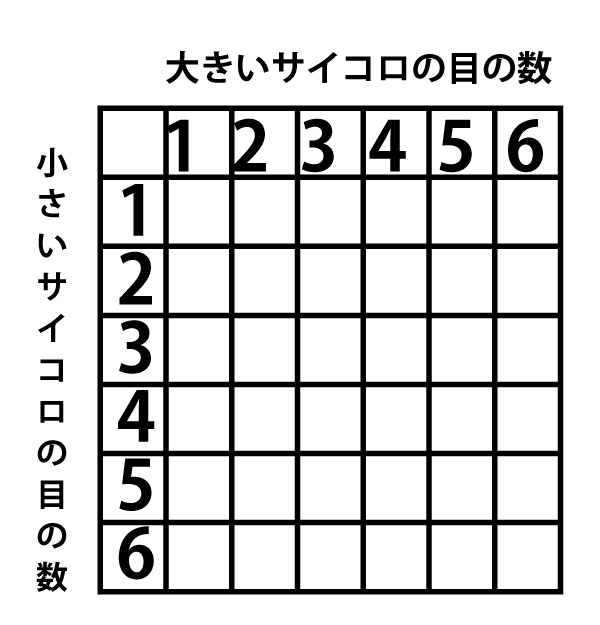
１、大小２つのサイコロをふる場合の出る目の場合の数

この表のように場合の数は、６×６＝36通りとなる。（大、小）＝（１、１）のように同じ数が出ることもありうるし、（大、小）＝（１、2）と、（大、小）＝（2、1）は別の出方なので、上のゴバン目表の全36マズが場合の数となる。

「１～6の2枚のカードを1回引き、そのカードをもとに戻してもう1回引く」場合も、（1回目、2回目）＝（1,1)がありうるし、（1,2)と（2,1)は別の出方なので、36通りである。

2、１～６のカードを2枚順に引く場合の数（1枚目は戻さない）


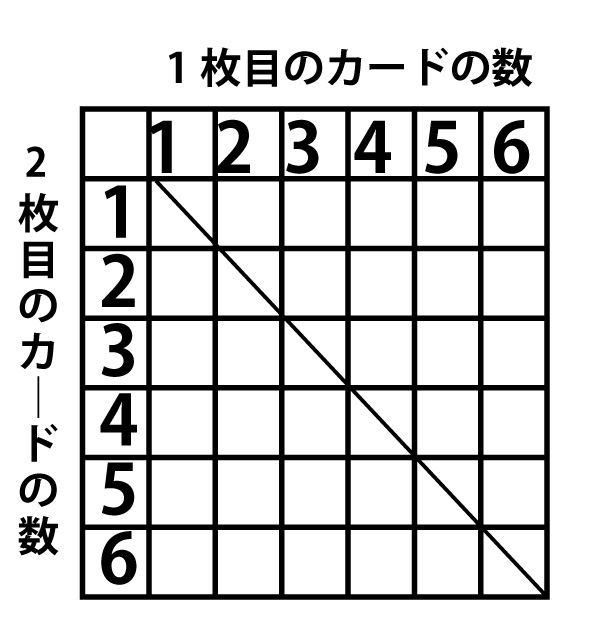
1枚目に引いたカードは戻さないので、2枚目にはひけない。よって上図のように30通りとなる。
（1枚目、2枚目）＝（1,2)と（2,1)では異なる場合の数である。
６（1枚目にひけるカードの場合の数）×５（2枚目にひけるカードの場合の数、1枚目のものは再び引けないので５となる）＝30通りである。

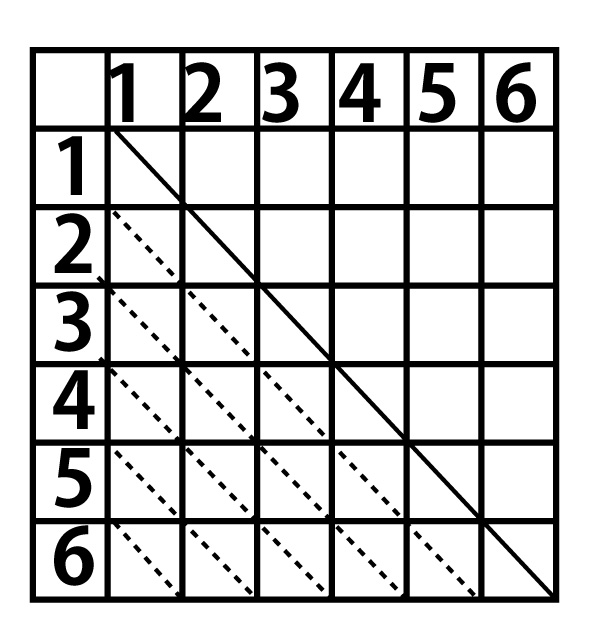
3、１～６のカードを同時に2枚引く場合の数

同時に2枚引く場合、順に引く場合とことなり（1回目、2回目）＝（１、２）と（2，1）は同じ場合の数となるので、ゴバン目の半分は同じとみなされるので、15通りとなる。

高校に行くと、この３つのパターンは、以下の記号と共に計算方式・原理を学ぶ。

中学（高校入試）では、この原理までは学ばないが、入試の時は、とにかくゴバン目を書いて、ありうる場合の数（ゴバンの数）を数えればよい。

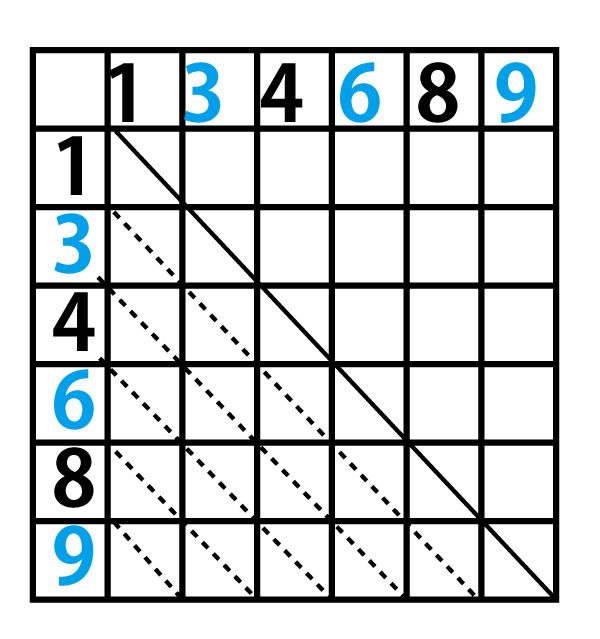
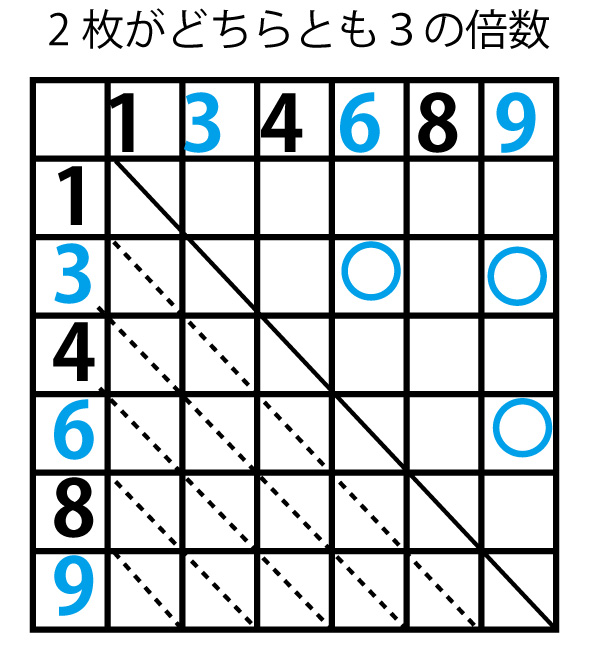
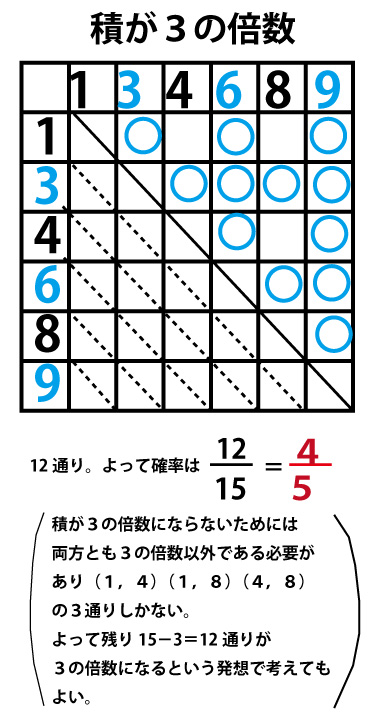
本設問については「３、2枚のカードを同時に引く」に相当し以下のようになる。場合の数全体は15通りである。解きやすいように本設問で重要な「３の倍数」を青字にした。（入試本番では色鉛筆は使えないので数字を〇で囲むなどして強調すると見やすい。）

（６と９の下の下線はカードが斜めになったりひっくりかえってもどちらか区別できるようにするための下線である）

【答】３通り