2023年大学入試共通テスト数学１A第3問（選択、場合の数、選択20点）問題・解答・解説

2023年12月14日　予備校講師・船橋市議　朝倉幹晴

2023年大学入試共通テスト「数学１A」第3問（選択、配点20点）の解答・解説を作成しましたので、ご活用ください。問題文の最後の所でページ番号「２」をクリックすると解答・解説に飛びます。

2023年大学入試共通テスト「数学IA」第3問（選択、20点）

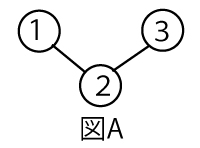
番号によって区別された複数の球が、何本かのひもでつながれている。ただし、各ひもはその両端で二つの球をつなぐものとする。次の条件を満たす球の振り分け方（以下、球の塗り方）を考える。
条件
・それぞれの球を、用意した５色（赤、青、黄、緑、紫）のうちのいずれか1色で塗る。
・1本のひもでつながれた二つの球は異なる色になるようにする。
・同じ色を何回使ってもよく、また使わない色があってもよい。

例えば図Ａでは、三つの球が2本のひもでつながれている。

この三つの球を塗るとき、球１の塗り方が5通りあり、球１を塗った後、球２の塗り方は4通りあり、さらに球３の塗り方は４通りある。したがって、球の塗り方の総数は80である。

（1）図Bにおいて、球の塗り方はアイウ通りある。
（2）図Cにおいて、球の塗り方はエオ通りある。
（3）図Dにおける球の塗り方のうち、赤をちょうど2回使う塗り方はカキ通りある。
（4）図Eにおける球の塗り方のうち、赤をちょうど3回使い、かつ青をちょうど2回使う塗り方はクケ通りある。

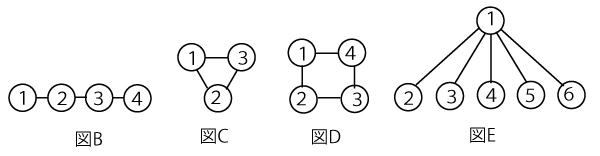
（5）図Dにおいて、球の塗り方の総数を求める。
そのために、次の構想を立てる。

構想
図Dと図Fを比較する。

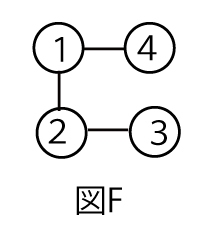
図Fでは球３と球４が同色になる戻り色が可能であるため、図Dよりも図Fの球の塗り方の総数の方が大きい。
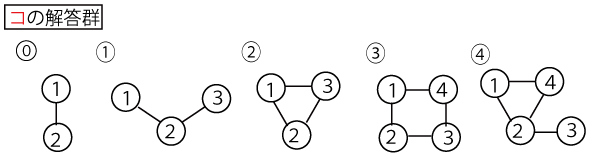
図Fにおける球の塗り方は、図Bにおける球の塗り方と同じであるため、全部でアイウ通りある。そのうち球３と球４が同一が同色になる球の塗り方の総数と一致する図として、のうち正しいものはコである。したがって、図Dにおける球の塗り方はサシス通りある。

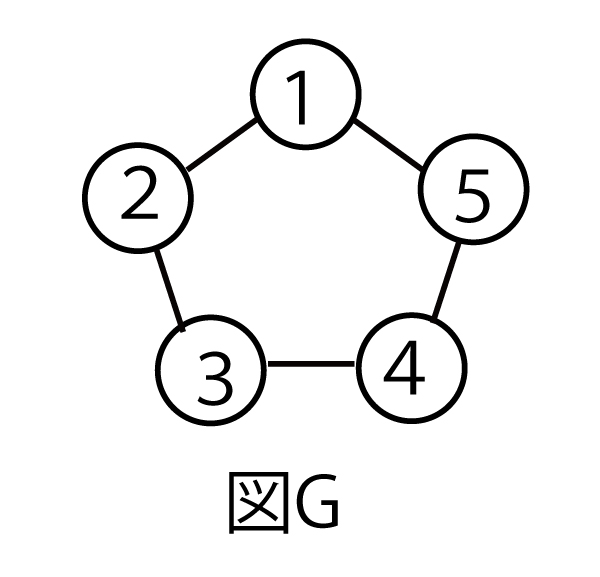
（6）図Gにおいて、球の塗り方はセソタチ通りある。

[next_p]