2023年大学入試共通テスト数学１A第3問（選択、場合の数、選択20点）問題・解答・解説

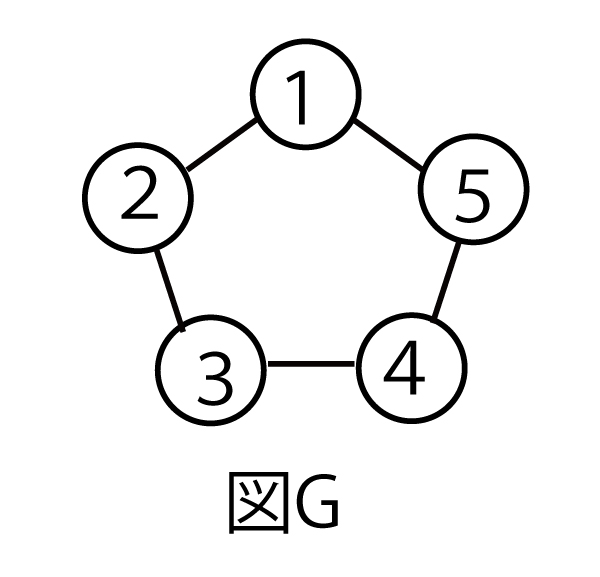
（1）図Bでは、１には５色の色を塗ることができる。２には１の色以外の４色、３には２の色以外の4色、４には３の色以外の４色を塗ることができるので、
５×４×４×４＝320通り（アイウ答）（3点）
（2）図Cで、お互いひもでつながれているので異なる色でないといけない。１の色を最初に塗ると考えると５色。２の色を次に塗ると１の色以外の4色、３の色は、１・２の色以外の３色なので
５×４×３＝60通り（エオ答）（3点）
（3）図Dで、赤は隣りあわないので、１赤・３赤か２赤・４赤である。
１・３赤の場合、２と４には赤以外の４色をそれぞれ塗ることができるので　　４×４＝16通り。
同様に、２・４赤の場合、１と３には赤以外の４色をそれぞれ塗ることができるので　　４×４＝16通り。
16＋16＝32通り　（カキ答）（3点）

（４）図Eで、赤で１を塗ってしまうと、２・３・４・５のいずれかの２球に赤を塗らなくてはならず条件と矛盾する。また青で１を塗ってしまうと、２・３・４・５のいずれかの１球に赤を青を塗らなくてはならず条件と矛盾する。
よって、１は赤・青以外の３色。
その場合２・３・４・５・６の３球に赤、2球に青を塗ることになる。
赤を塗る３球を選べば、残り２球は自動的に青に決まるので、５球から赤になる3球を選ぶ組合せ

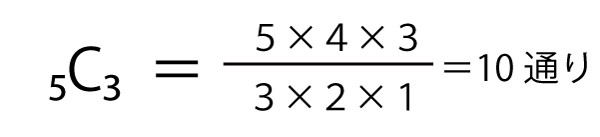
３（１の色）×10（２～６の赤・青の塗り方）＝30通り　（クケ答）（3点）

（5）
図Fでは球３と球４が同色になる戻り色が可能であるため、図Dよりも図Fの球の塗り方の総数の方が大きい。
図Fにおける球の塗り方は、図Bにおける球の塗り方と同じであるため、全部でアイウ（320）通りある。図Fのうち、球３と球４が同一が同色になる球の塗り方の総数と一致する図は、

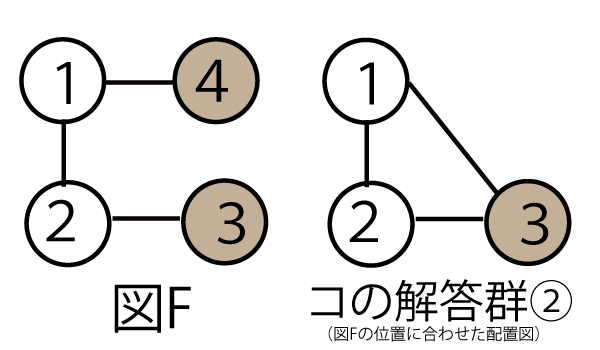
図Fで３と４が同色ということは、１も２も、３の色（４と同色）になれないとので、コの解答群では（3点）の塗り方（と同じ総数である。

図Ｄの塗り方総数＝図Ｂの塗り方総数ー図C（コの選択肢）の塗り方総数
＝320ー60＝260

したがって、図Dにおける球の塗り方はサシス（260）（サシス）通り（2点）ある。

（6）

（５）の発想の延長上に、
ｎ個の「数珠」の塗り方の総数
＝ｎ個の「鎖」の塗か方の総数ー（ｎ－1）個の「数珠」の塗り方の総数

と考えられる。

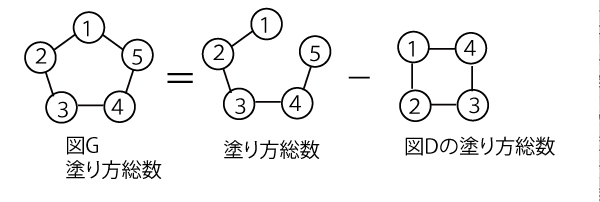
１ー２ー３ー４ー５は（1）と同様に考え
５通り×４通り×４通り×４通り×４通り＝1280
（5）より図Ｄの塗り方の総数は260

よって1280ー260＝1020（セソタチ答）（3点）