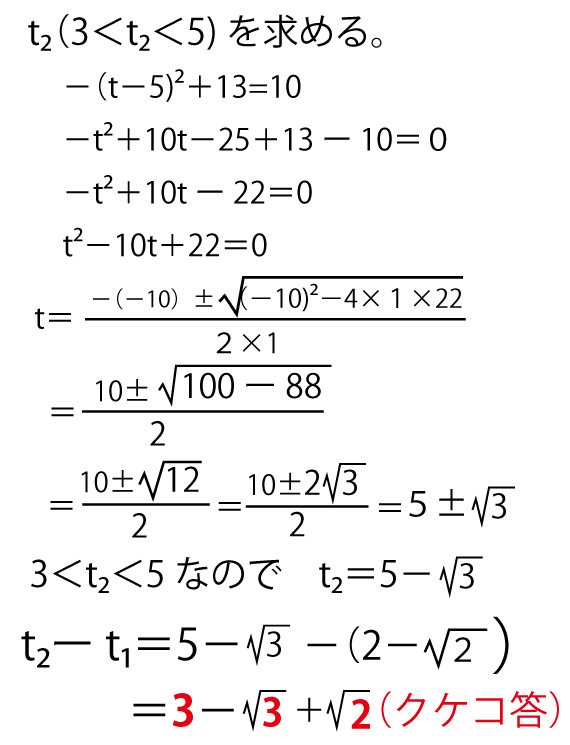2024年　＃大学入試　＃共通テスト　＃数学1A 第2問［１］（配点15点）問題・解答・解説

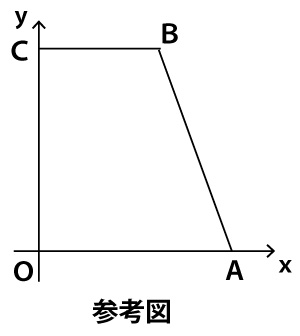
【解説】
（1）ア（△PBQの面積）
Bからx軸に下ろした垂線のx軸との交点をHとする。

△PBQ（上図青）の面積は、長方形OCBHの面積から、青を取り囲む白い３つの三角形△OPQ、△CBQ、△BPHの面積を引いたものである。

長方形OCBH＝４×６＝24
△OPQ＝１／２　×１×４＝２
△CBQ＝１／２　×２×４＝４
△BPH＝１／２　×３×６＝９
よって
24ー（２＋４＋９）＝９（ア答）

（2）

３秒以内ならば、PはHよりｘ座標が小さいので（1）と同じ考え方ができる。
ｔ秒後のＰのx座標はｔ、Ｑのｙ座標は（6ー2t）である。

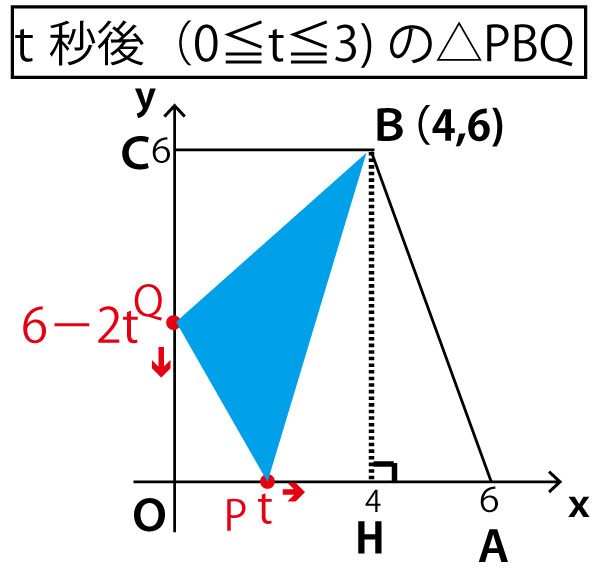
よって
長方形OCBH＝４×６＝24
△OPQ＝１／２　×t×(6ー2t)＝3tーt²
△CBQ＝１／２　×2t×４＝4t
△BPH＝１／２　×(4ーt)×６＝12ー3t
よって
△PBQ＝24ー（3t－t²＋4t＋12ー3t)
=24ー（－t²＋4t＋12）
＝24＋t²ー4t－12
=t²−4t＋12
＝t²−4t＋4－4＋12
＝（t－2)²＋８
t＝２の時最小値８（イ答）
二次関数の軸はｔ＝２であり、0≦t≦3の範囲で、最大値をとるのは軸からもっとも離れたｔ＝０の時である。よって　（0-2)²＋8=4+8＝12（ウ答）

【参考】△PBQが最大値をとるｔ＝０の時の△ＰＢＱ（＝△ＯＢC)

（3)
規則で、PはAに到達した時点で移動が終了する。毎秒１で長さ６のOAを移動するので移動終了は６秒後である。
同様に、規則でQはO到達後、Cに戻った時点で移動が終了する。C→Oは６、O→Cは６なので、移動距離の合計は12。毎秒２で移動するので移動終了は６秒後である。
したがって、（1）で０≦ｔ≦３を考えているので、3＜ｔ≦６を考えればよい。

3＜t≦6では、（４≦ｔとなる部分があるので、長方形OCBHではなく）台形OCBAから、３つの三角形△OPQ、△CBQ、△BPAの面積を引いたものである。またＰは3秒でOを折り返し、Cに向け毎秒２でｙ座標が大きくなるので、ｙ座標は2(t－3)。

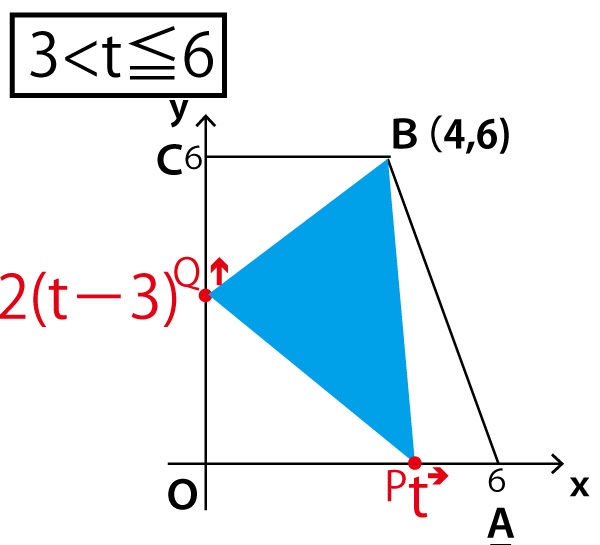
台形OCBA＝1／２　×（４＋６）×６＝30
△OPQ=1／2   ×t×2(tー3)＝t²−3t
△CBQ＝１／２　×4×[6－2(tー3)]＝1／２　×4×（12ー2t）＝24－4t
△BPA＝１／２　×(6−t)×６＝18ー3t

△PBQ＝30ー（t²ー3t＋24ー4t＋18ー3t）＝－t²＋10ｔ－12

＝－t²＋10ｔー25＋25ー12

＝－（t²−10t＋25）＋25ー12
＝－(t－5）²＋13
ｔ＝５の時、最大値13
軸はx=5なので、軸からもっとも離れたｔ＝３の時最小値となり、９。（ｘ＝３は含まないが含まれたと考えた場合の最小値）

（1）（０≦t≦３）の範囲では、最小値８、最大値12
（2）（３＜t≦６）の範囲では、最小値９（ｔ＝３の場合）、最大値13

あわせて考えた全範囲では、最小値８（オ答）、最大値13（カキ答）

（4）
（2）（3）で求めた△PBQの面積（Ｓとする）の0≦ｔ≦３と３＜ｔ≦６の範囲での二次関数をつなげて描くと以下のようになる。

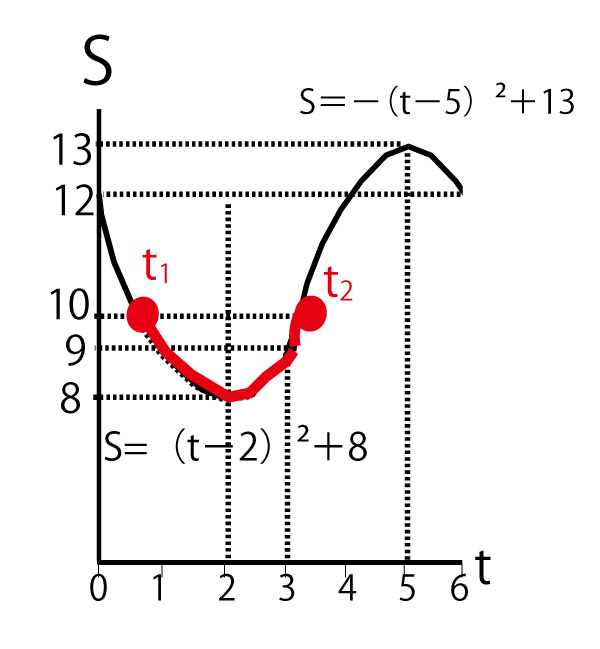
10以下になる範囲はつながっているので
Ｓ=(t－2)²＋８で、Ｓ＝10となるt₁（t₁＜2)をもとめ、
Ｓ＝－（t－5)²＋13で、S=10となるt₂（3<t₂＜５）をもとめ
t₂ーt₁を求めればよい。