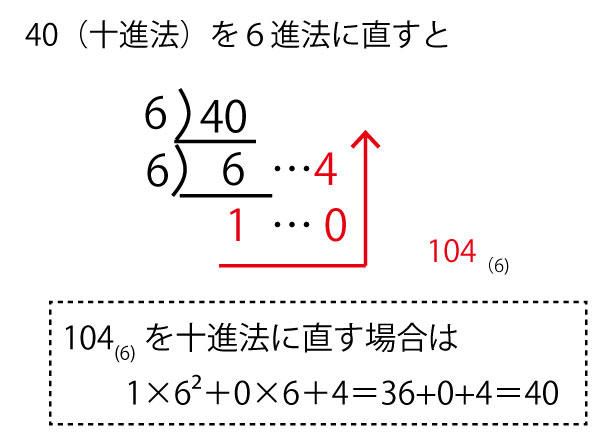
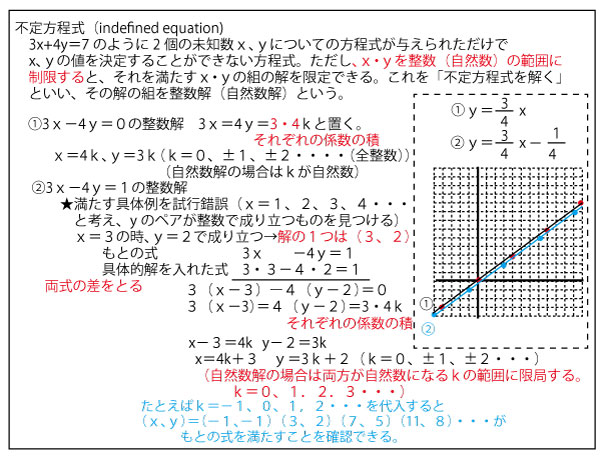
2024年　＃大学入試　＃共通テスト　「＃数学IA」第4問（選択・計20点）問題・解答・解説

【2024年数学IA第4問解答】（計20点）
アイウ104（2点）　エオカ103（3点）　キク64（2点）　ケコサシ1728（3点）
スセ64、ソ６（あわせて3点）　　タチツ518（4点）　テ（3点）

【解説】

アイウ104

10011₍₂₎を十進法に直すと、
１×2⁴＋1×2＋１＝16＋2＋１＝19

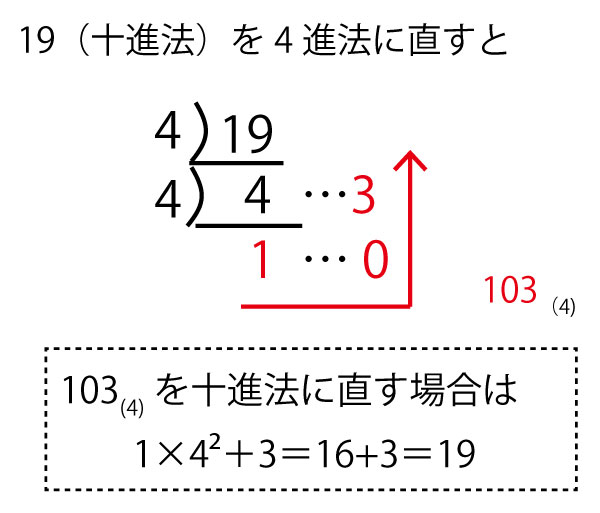
エオカ103

（2）

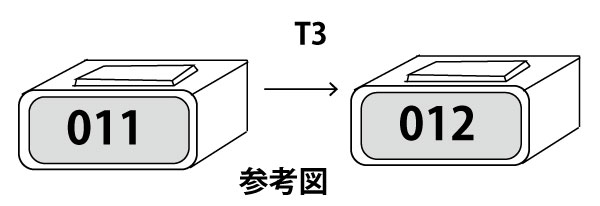
T３の３進法では
計算で考える場合は、1000(3)を十進法に直し１×３³＝27個で一巡する。

列挙表記すると
000、001、002、010、011、012、020、021、022、（十進法で9個）
100、101、102、110、111、112、120、121、121、122、（十進法で9個）
200、201、202、210、211、212、220、221、222、（十進法で9個）
1000（リセットされて000）

T４の４進法では
計算で考える場合は、1000(4)を十進法に直し１×4³＝64個（秒）で一巡する。
キク64

列挙すると
000、001、002、003、010、011、012、013、020、021、022、023、030、031、032、033
（十進法で16個）
100、101、102、103、110、111、112、113、120、121、122、123、130、131、132、133
（十進法で16個）
200、201、202、203、210、211、212、213、220、221、222、223、230、231、232、233
（十進法で16個）
300、301、302、303、310、311、312、313、320、321、322、323、330、331、332、333
（十進法で16個）
1000（リセットされて000）

同様に5進法では1000_（5)で、1×5³＝125個（秒）で一巡する。
同様に6進法では1000_（6)で、1×６³＝216個（秒）で一巡する。

T4とT6が同時にスタートし、初めて両方の表示が000に戻るのは
64（4³）と216（6³)の最小公倍数なので、
４³＝2⁶と6^３＝2³・3³の最小公倍数なので、
2⁶・3³＝64・27＝1728（ケコサシ）

T3は27秒で一巡し、012となるのは000から１×3＋2＝5秒後。
つまり27x＋5（xは整数）に、012と表示される。

Ｔ4は64（スセ）秒で一巡し、012となるのは000から1×4＋2＝6秒後（ソ答）
つまり64y＋6（yは整数）に、012と表示される。

27x＋5＝64y＋6となればよい。
27xー64y＝１・・・（ア）
これに当てはまる最小のx、yを考えればよい。

(ア）ー（イ）より
27（ｘー19）ー64（ｙー８）＝０
27（ｘー19）＝64（y－8）

よってこれを満たす最小のｘ＝19、ｙ＝８

よって27ｘ＋５＝27・19＋５＝518（タチツ答）
（あるいは64y+6＝64・8＋6＝518）

＜参考＞

T4で012と表示されるのは、前問の通り64y＋6秒後（yは０以上の整数）
T6で012と表記されるのは216ｚ＋６＋２＝216ｚ＋８秒後（ｚは０以上の整数）

64ｙ＋６＝216z＋８
64ｙー216ｚ＝２
32ｙー108ｚ＝１

32ｙと108ｚは偶数でその差が１であることはないので、この式を満たすｙ、ｚは存在しない。したがって、（Ｔ4とT6を同時にスタートさせてから、両方が同時に012と表示されることはない。）