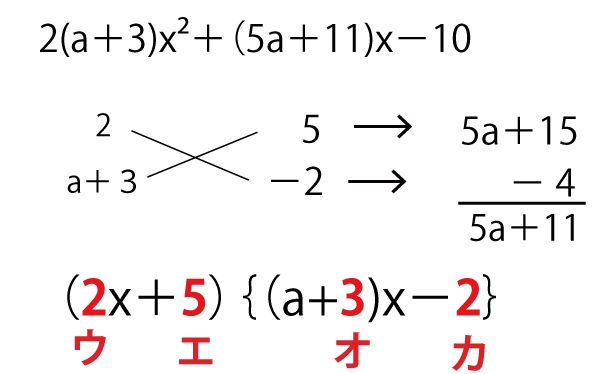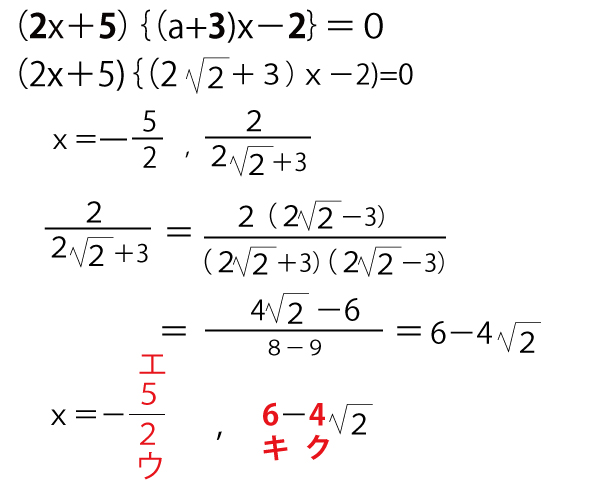2025年大学入試共通テスト数学1A第1問［１］（配点10点）問題・解答・解説

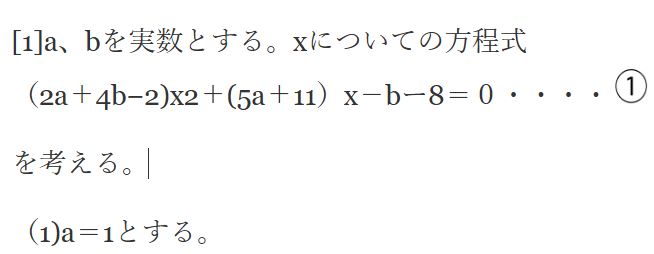
【解説】

[1]a、bを実数とする。xについての方程式
（2a＋4b−2)x²＋(5a＋11）x－bー8＝０・・・・

を考える。

（1)a＝1とする。
a=1を　の左辺に代入する。
（2a＋4b−2)x²＋(5a＋11）x－bー8
＝（2×1＋4b−2)x²＋(5×1＋11）x－bー8
＝4bx²＋16x－b−8
bに着目すると、の左辺は
（4x²−１）b＋16x－８・・・・

と表せる。よって、を因数分解すると
（2x－1)（2x＋１）b＋8(2x－1)
（2x－1)（2（ア答）bx＋b+8（イ答））
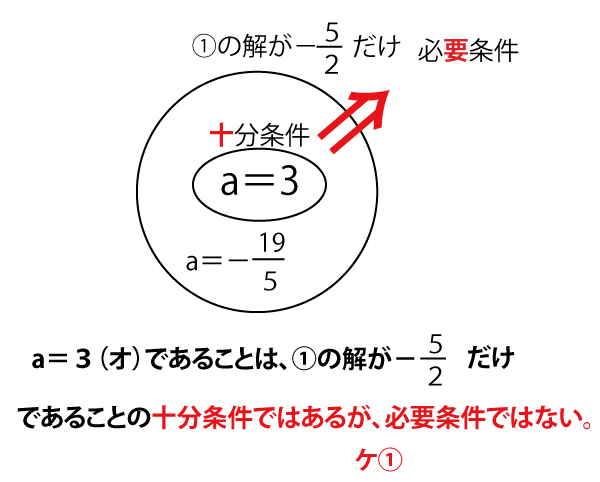
したがって、はの解の一つであることがわかる。

（2)b＝２のとき
b=2を①の左辺に代入する
（2a＋4b−2)x²＋(5a＋11）x－bー8
＝(2a＋4×2－2)x²＋（5a＋11）x－2−8
＝（2a＋6)x²＋（5a＋11)ｘ－10
＝2(a＋3)x²＋（5a＋11)x－10

（ii)のとき、の解は