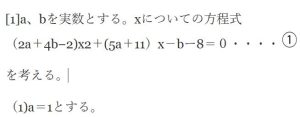2025年大学入試共通テスト「数学1A」第1問［２］（20点）問題・解答・解説
asakura
2025年4月28日 朝倉幹晴（予備校講師・船橋市議）
2025年大学入試共通テスト「数学1A」の第1問［2］（配点20点）の解答解説を作成しました。学習・入試対策にご活用ください。このページを最後までスクロールし、[２]をクリックすると、解答・解説のページに飛びます。
2025年大学入試共通テスト「数学１A」問題・解答・解説
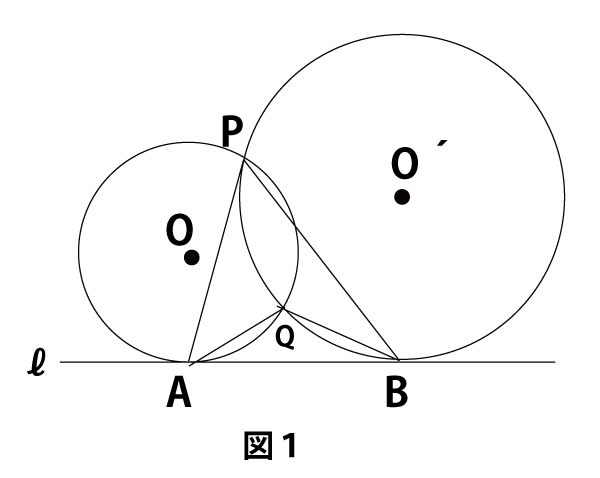
第1問［２］図１のように、直線ℓ上の点Aにおいてℓに接する半径２の円を円Oとし、ℓ上の点Bにおいてℓに接する半径4の円を円O´とする。円OとO´は2点で交わるとし、その交点をP、Qとする。ただし、∠APB＜∠AQBとする。さらに、∠PABは鋭角であるとする。このとき、△PABと△QABについて考えよう。
（1）∠PAB＝α、∠PBA＝βとおく。
円Oの中心Oから直線PAに引いた垂線と直線PAとの交点をHとする。∠OAB＝90°であるから、∠AOH＝αである。よって、△OAHに着目すると、AH＝コsinαであるから
PA＝2AH＝サsinα・・・・
（コサあわせて2点）
である。
同様にして、円O´の中心O´から直線PBに引いた垂線と直線PBとの交点をH´とすると
PB＝2BH´＝シsinβ・・・・
であることもわかる。
（2）太郎さんと花子さんは、（１）の考察を振り返っている。
太郎：△QABの外接円の半径も求められるかな。
花子：（1）のR１の求め方を参考にすればよさそうだね。
△PAB、△QABの外接円の半径をそれぞれ、R１、R２とおく。
このとき、R1ツR２である。さらに、sin∠APBテsin∠AQBであることもわかる。
（3）太郎さんと花子さんは、これまでの考察をもとに、△PABと△QABの辺の長さについて考えている。
太郎：ABの長さが考えられれば、PAとQAの長さが求められそうだね。
花子：∠AFB＜∠AQBに注意して求めてみようよ。
