2025年千葉県公立高校入試「数学」第4問問題・解答・解説（配点18点）

2026年1月8日（木）　　船橋市議（無党派）・予備校講師　朝倉幹晴

2025年2月に行われれた千葉県公立高校入試数学第4問（総合問題、配点18点）の問題・解答・解説を作成しました。普段の学習や2026年2月の千葉県公立高校入試、他県・私立の高校入試対策にお役立てください。なお、千葉県教育委員会が発表した正答率・無答率も付記しました。

問題ページの最後で「２」をクリックすると解答・解説のページに飛びます。

2025年第4問（配点15点）

次の会話文を読み、会話文中の「の」～「も」について、あとの（1)～（6)の問いに答えなさい。ただし、円周率をπとする。

会話文

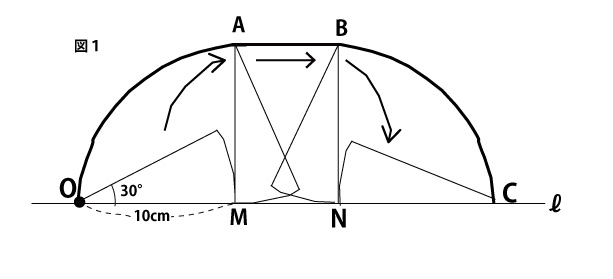
教師T：おうぎ形と円錐を、それぞれすべらないように転がしたときについて考えましょう。図１の太線部分は、半径OMが10cmで中心角が30度のおうぎ形を、直線ℓ上ですべらないように転がしたとき、点Oが移動した跡（あと）を表しています。点A、B、M、Nは、∠OMA＝∠ONB＝90°となる点です。点Cは、直線ℓ上にあり、おうぎ形を転がし終わった後の点Oの位置を表しています。このとき、図１の点Oから点Cまでの太線部分の長さを求めてください。

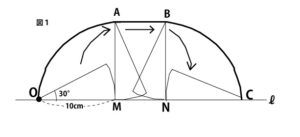
生徒S：まず、点Oから点Aまでの太線部分の長さはのπcm（3点）（正答率74.8%、無答率5.8%)です。この長さと、点Bから点Cまでの太線部分は同じ長さです。
教師T：そのとおりでです。
生徒S：次に点Aから点Bまでの太線部分は、直線ℓからの距離が常に10cmとなるので線分になります。また、直線ℓ上ですべらないように転がしているので、線分ABの長さはおうぎ形の弧の長さに等しいです。よって、点Oから点Cまでの太線部分の長さは（3点）（正答率28.8%、無答率22.3%)です。

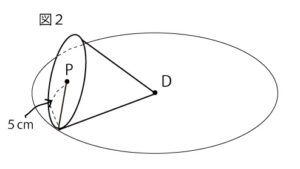
教師T：正解です。では、次の問題です。図２のように、頂点D、半径5cmの円Pを底面とする円錐を、点Dを中心として平面上ですべらないように転がりました。このとき、円Dの上を１周して、もとの位置にもどるまでに、円錐はちょうど2回転しました。この円錐の母線の長さは何cmですか。

生徒Ｓ：円Ｐの周の長さと円Ｄの周の長さの関係から、円錐の母線の長さはへほcm（3点）（正答率57.7%、無答率15.5%)です。
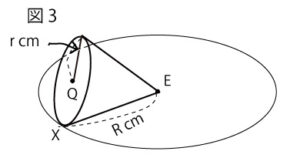
教師Ｔ：すばらしいです。また、図３のように、頂点Ｅ、底面が半径rcmの円Ｑで、母線の長さがＲcmの円錐を、点Ｅを中心として平面上ですべらないように転がしました。点Ｘは、円錐を転がす前の、円Ｑが円Ｅに接している点を表しています。ｒとＲの値を変えながら、点Ｘの動きを考えてみましょう。
例えば、r=2、R=8とすると、円錐の点Ｘは、円錐がちょうど４回転したときに円Ｅの上を1周し、もとの位置に戻ります。しかし、r=9、R=24とすると、円錐が何回か回転して円Ｅの上を１周したとき、円錐の点Ｘはもとの位置にはありません。では、r=9、Ｒ＝24のとき、円錐の点Ｘが初めてもとの位置に戻るのは、円錐が円Ｅの上を何周したときですか。

生徒Ｓ：円Ｅの上をま周（3点）（正答率30.7%、無答率18.4%)したときに初めてもとの位置に戻ります。
教師Ｔ：正解です。さて図３の円錐の点Ｘにインクをつけて、点Ｘが初めてもとの位置に戻るまで円錐を転がしたところ、点Ｘが接した円Ｅの周上に、インクの跡が残りました。r=2、Ｒ＝８のとき、もとの位置を含めてインクの全部で４個残りました。それでは、ｒ＝９、Ｒ＝24のとき、インクの跡は全部で何個残りますか。ただし、インクの跡は点Ｘが接した円Ｅの周上に必ず点として残るものとします。
生徒Ｓ：もとの位置を含めて、インクの跡は全部でみ個（3点）（正答率20.1%、無答率24.2%)残ります。
教師Ｔ：正解です。さらに、ｒ＝９、Ｒ＝21のとき、円錐を転がす前の点Ｘの位置を点X0として、円錐を転がしたときにできたインクの跡を、跡ができた順に、点Ｘ1,X2,X3,・・・とすると、∠X5EX0と大きさは何度になりますか。ただし、０度以上180度以下とします。
生徒S：むめも度（3点）（正答率12.6%、無答率41.6%)です。rとRの値を変えれば、他にもおもしろい問題ができそうです。

（1）「の」にあてはまるものを答えなさい。（3点）（正答率74.8%、無答率5.8%)

（2)「ほ」～「ふ」にあてはまるものをそれぞれ答えなさい。（3点）（正答率28.8%、無答率22.3%)

（3)「へ」「ほ」にあてはまるものをそれぞれ答えなさい。（3点）（正答率57.7%、無答率15.5%)

（4）「ま」にあてはまるものを答えなさい。（3点）（正答率30.7%、無答率18.4%)

（5）「み」にあてはまるものを答えなさい。（3点）（正答率20.1%、無答率24.2%)

(6)「む」～「も」にあてはまるものをそれぞれ答えなさい。（3点）（正答率12.6%、無答率41.6%)