2025年千葉県公立高校入試「数学」第3問（図形の証明）問題・解答・解説（配点16点）

2026年1月8日（木）　　船橋市議（無党派）・予備校講師　朝倉幹晴

2025年2月に行われれた千葉県公立高校入試数学第3問（図形の証明、配点16点）の問題・解答・解説を作成しました。普段の学習や2026年2月の千葉県公立高校入試、他県・私立の高校入試対策にお役立てください。なお、千葉県教育委員会が発表した正答率・無答率も付記しました。

問題ページの最後で「２」をクリックすると解答・解説のページに飛びます。

2025年第3問（計16点）

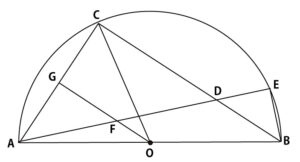
図のように、線分ABを直径とする半円Oがある。弧AB上に、∠AOCが鋭角となるように点Cをとり、線分BC上に2点B、Cとは異なる点Dをとる。直線ADと弧ABとの交点で、点Aとは異なる点をEとし、点Bと結ぶ。また、∠AOCの二等分線と線分AE、ACとの交点をそれぞれF、Gとする。
このとき、次の（1)～（3)の問に答えなさい。

（1）次の（a)(b)(c)に入る最も適当なものを選択肢ア～カのうちからそれぞれ１つずつ選び、符号で答えなさい。

線分OAと線分（a)は、半円Oの（b)だから長さが等しい。よって、△OCAは（c)である。

選択肢
アOC　ィAB　ウ直径　エ半径　オ二等辺三角形　カ直角三角形
（完答で5点）（正答率79.5%、無答率0.2％）

（2）△GAF∽△EBDとなることを証明しなさい。
ただし、（1）の「線分OAと線分（a)は、半円Oの（b)だから長さが等しい。よって、△OCAは（c)である。」のことがらについては、用いてもかまわないものとする。

（6点）（6点配点11.4%、3点配点5.1％、無答率40.0%)
（3)次の「な」～「ね」にあてはまるものをそれぞれ答えなさい。
OA＝CA＝6cm、BD:DC＝1:2であるとき、
△EBDの面積は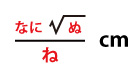　である。

（5点)(正答率2.0%、無答率52.9%)