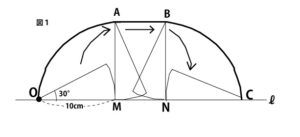
2025年千葉県公立高校入試「数学」第3問(図形の証明)問題・解答・解説(配点16点)

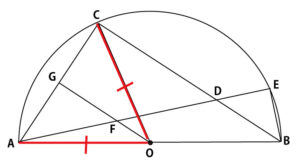
線分OAと線分OC(ア)(a答)は、半円Oの半径(エ)(b答)だから長さが等しい。よって△OCAは二等辺三角形(オ)(c答)である。
(2)
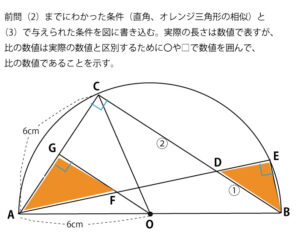
図でオレンジの2つの三角形が相似であることの証明が求められている。
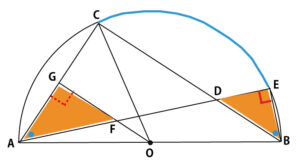
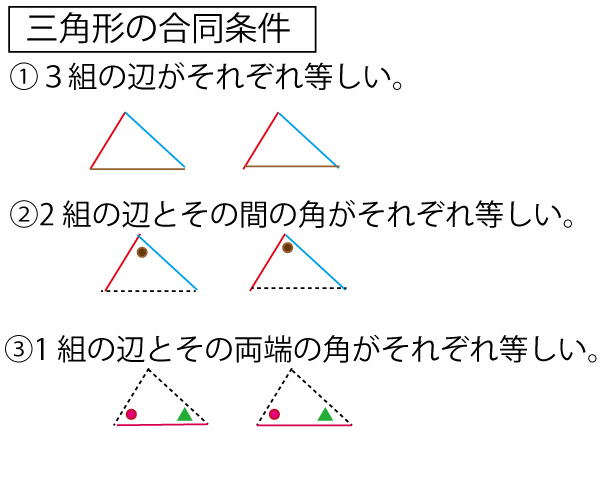
三角形の相似条件は、「2組の角がそれぞれ等しい」「2辺の比とその間の角がそれぞれ等しい」「3辺の比がそれぞれ等しい」であるが、本設問では辺の長さの比の情報はなく、「2組の角がそれぞれ等しい」を使うことが予測される。(千葉県公立高校入試の三角形の相似の証明の問題では「2組の角がそれぞれ等しい」を使うことが最も多い)
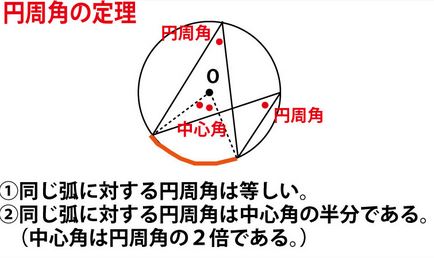
まず、図で青で示した弧CEに対する円周角であることに気づけば、1組目(∠GAF=∠EBD)の気づく。
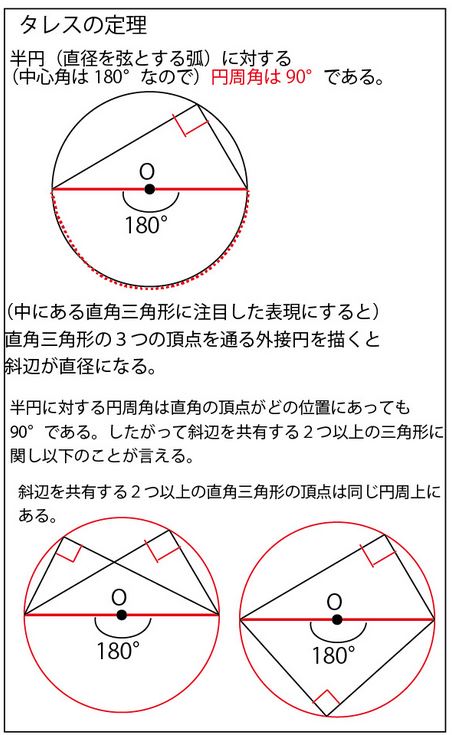
次に直径ABを弦とする半円の弧に対する円周角は90°(タレスの定理)なので、∠DEB=90°
∠FGAは90°のように見えるが、はっきりと書いていないので、ここを前問(1)から、90°であることを証明する。
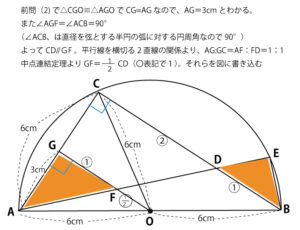
そこで以下、灰色の2三角形が合同であることを証明する。
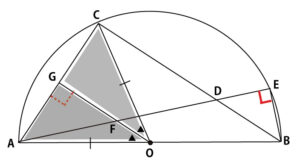
前問(1)よりOC=OA、OGは∠AOCの二等分線なので∠COG=∠AOG、OG=OGで2辺とその間の角が等しいので
△OCG≡△OAG。よって∠CGO=∠FGA(∠AGO)=90°
この証明により∠FGA=90°とわかり、∠FGA=∠DEB=90°で、2組目の角も等しいことが証明でき、
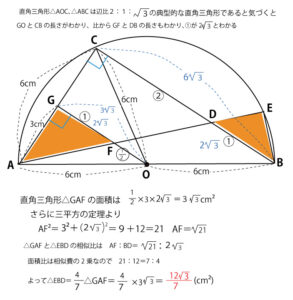
△GAF∽△EBDが証明できる。
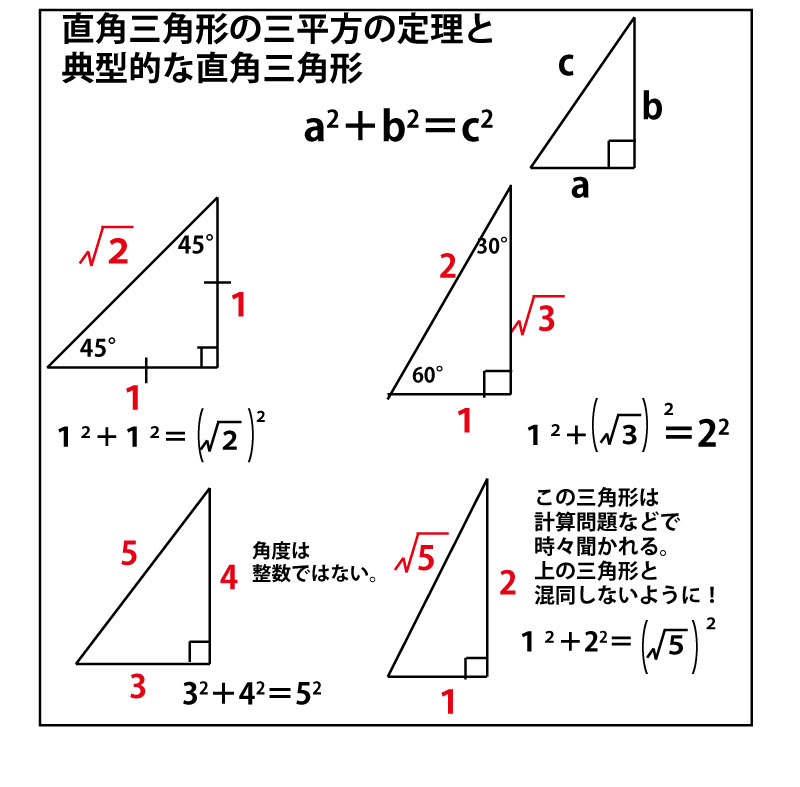
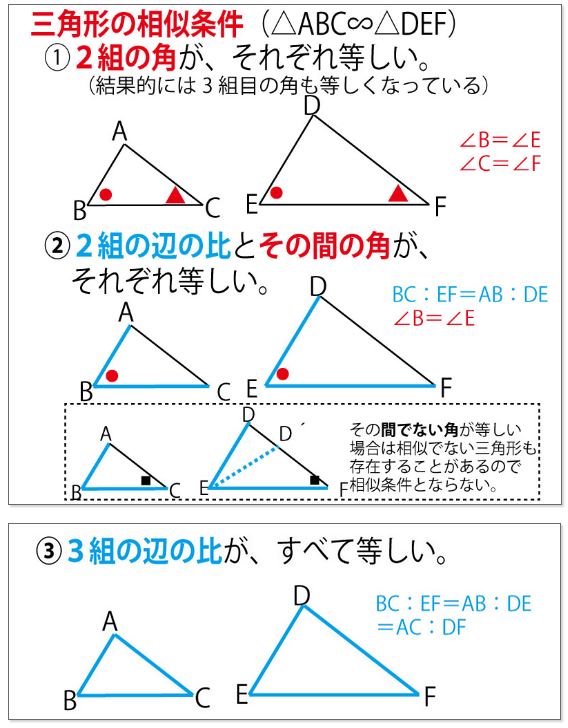
★図形の証明や計算に使う定理(一部)
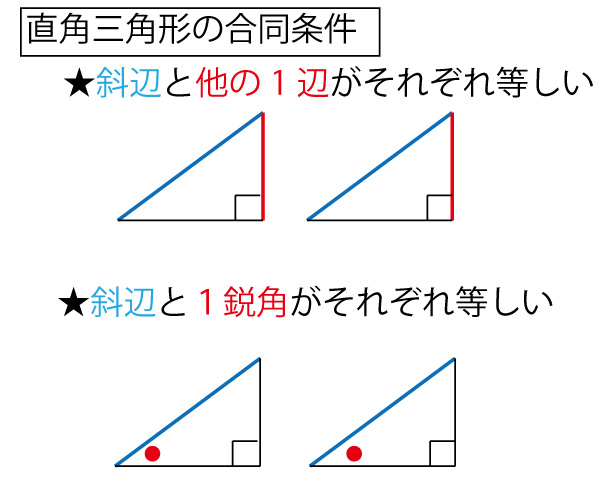
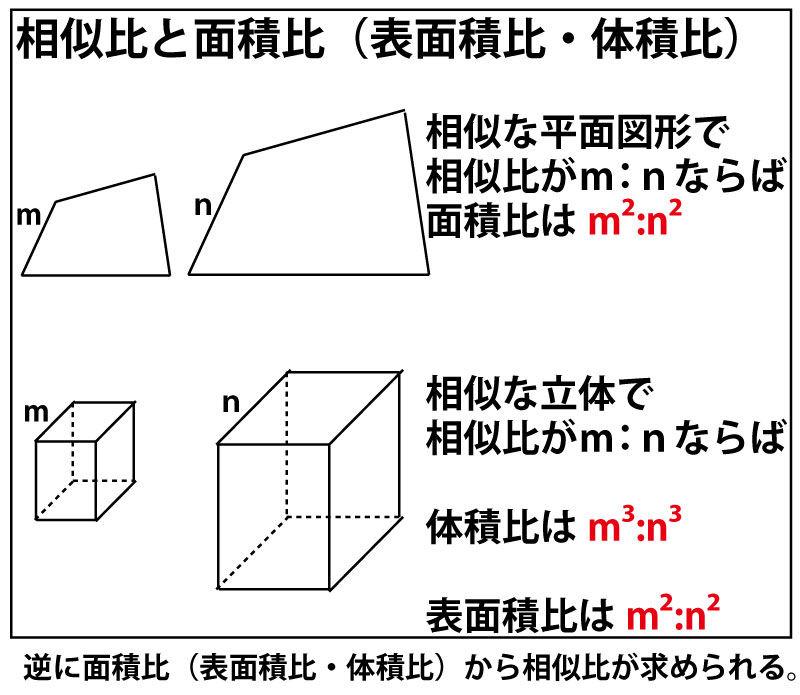
三角形の相似条件を確認しましょう。
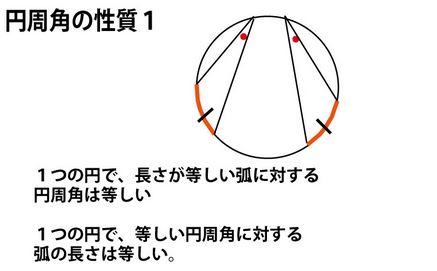
★参考 円周角の定理と円周角の性質1~4
★参考 拙著「図形の証明」(他3著作)、アマゾンでお求めいただけます。